题目内容
设f（x）=-x，g（x）=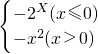
，则方程f[g （x）]-2=0的解是________．
x=
分析：由已知，f[g （x）]=2，∴g （x）=-2，转化成知道分段函数g （x）的函数值，求x的问题．逐段寻求，最后取并．
解答：将g（x）看作整体，由已知g （x）=-2，
当x≤0时，由-2x=-2，得x=1，与x≤0矛盾．舍去．
当x＞0时由-x2=2得x=（舍去x=-）
故答案为：
点评：本题考查复合函数概念，分段函数求值，分类讨论思想．在解决分段函数问题时，一定要注意自变量的值所在范围即其相应的解析式．
分析：由已知，f[g （x）]=2，∴g （x）=-2，转化成知道分段函数g （x）的函数值，求x的问题．逐段寻求，最后取并．
解答：将g（x）看作整体，由已知g （x）=-2，
当x≤0时，由-2x=-2，得x=1，与x≤0矛盾．舍去．
当x＞0时由-x2=2得x=
（舍去x=-）故答案为：
点评：本题考查复合函数概念，分段函数求值，分类讨论思想．在解决分段函数问题时，一定要注意自变量的值所在范围即其相应的解析式．
练习册系列答案
相关题目