Question

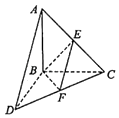
【题目】如图1所示，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别是边CD，CB的中点，EF∩AC=O，沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到如图2所示五棱锥P﹣ABFED，且AP= ，
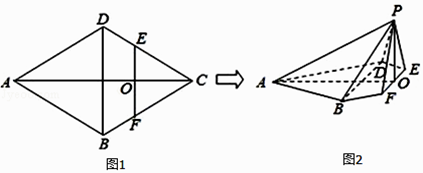
（1）求证：BD⊥平面POA；
（2）求二面角B﹣AP﹣O的正切值．

Answer 1

【答案】
（1）证明：PO⊥EF，AO⊥EF，所以EF⊥平面POA，因为BD∥EF

∴BD⊥平面POA

则PO⊥BD，又AO⊥BD，AO∩PO=O，AO平面APO，PO平面APO，

∴BD⊥平面APO

（2）解：因为AP= ，可证PO⊥AO，所以EF，PO，AO互相垂直

以O为原点，OA为x轴，OF为y轴，OP为z轴，建立坐标系，

则O（0，0，0），A（3 ，0，0），P（0，0， ），B（ ，2，0），

设 =（x，y，z）为平面OAP的一个法向量，

则 =（0，1，0）， =（x，y，z）为平面ABP的一个法向量，

=（﹣2 ，2，0）， =（﹣3 ，0， ），

则 ，令x=1，则y= ，z=3，

则 =（1， ，3）…．cosθ= = ，∴tanθ=

∴二面角B﹣AP﹣O的正切值为

【解析】（1）证明PO⊥BD，AO⊥BD，可得BD⊥平面APO，（2）以O为原点，OA为x轴，OF为y轴，OP为z轴，建立坐标系，则O（0，0，0），A（3 ，0，0），P（0，0， ），B（ ，2，0），求出平面OAP的一个法向量，平面ABP的一个法向量即可