题目内容
已知直线![]() 与曲线
与曲线![]() 交于A、B两点。
交于A、B两点。
(1)当![]() 时,有
时,有![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)当实数a为何值时,对任意![]() ,都有
,都有![]() 为定值
为定值![]() ?指出
?指出![]() 的值;
的值;
(3)是否存在常数![]() ,使得对于任意的
,使得对于任意的![]() ,
,![]() ,都有
,都有![]() 恒成立?
恒成立?
如果存在,求出的![]() 得最小值;如果不存在,说明理由。如果存在,求出的
得最小值;如果不存在,说明理由。如果存在,求出的![]() 得最小值;如果不存在,说明理由。
得最小值;如果不存在,说明理由。
(1)当![]() 时,则直线
时,则直线![]() 与曲线
与曲线![]() 的两交点分别
的两交点分别
为![]() , 由
, 由![]() , 解得
, 解得![]()
故曲线![]() 的方程是
的方程是![]()
(2)假设存在这样的常数a,由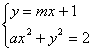 消去y
消去y
得:![]() 则有
则有 ![]()
![]()
![]()
![]()
![]() 关于
关于![]() 恒成立,则有
恒成立,则有
![]() 解得:
解得:![]() ,
,![]()
而当![]() 时,
时,![]() ,且方程判别式
,且方程判别式![]()
故当![]() 时,对任意
时,对任意![]() ,都有
,都有![]() ,此时
,此时![]()
(3)假设存在常数![]() ,使得对于任意的
,使得对于任意的![]() ,
,![]() ,
,
都有![]() 恒成立
恒成立
即![]() =
=![]()
当![]() 时, 只需
时, 只需![]() 成立, 即
成立, 即![]()
![]() 时,
时,![]() ,只需
,只需![]() , 即
, 即![]() ,
,
故![]() 的最小值是0。
的最小值是0。
故存在常数![]() ,使得对于任意的
,使得对于任意的![]() ,
,![]() ,都有
,都有![]() 恒成立,且
恒成立,且![]() 的最小值是0。
的最小值是0。

练习册系列答案
相关题目
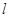 的极坐标方程为
的极坐标方程为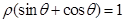 ,曲线
,曲线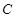 的参数方程为
的参数方程为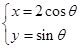 (
( 为参数).
为参数). ,求
,求 的面积.
的面积. 相切,点C在
相切,点C在 上.
上. 的直线与曲线交于A、B两点.问直线
的直线与曲线交于A、B两点.问直线 是以
是以 为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.
为直角的直角三角形?如果存在,求出点C的坐标;若不能,请说明理由.