题目内容
已知函数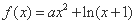 .
.
(1) 当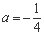 时,求函数
时,求函数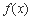 的单调区间;
的单调区间;
(2) 当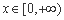 时,函数
时,函数 图象上的点都在
图象上的点都在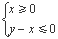 所表示的平面区域内, 求实数
所表示的平面区域内, 求实数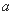 的取值范围.
的取值范围.
解:(1) 当.时,
 ,
,

 ,
,
由 解得
解得 ,由
,由 解得
解得 .
.
故函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 . (4分)
. (4分)
(2) 因函数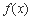 图象上的点都在
图象上的点都在 所表示的平面区域内,
所表示的平面区域内,
则当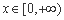 时,不等式
时,不等式 恒成立,即
恒成立,即 恒成立,、
恒成立,、
设 (
( ),只需
),只需 即可.
即可.
由
 ,
,
(i) 当 时,
时,  ,
,
当 时,
时, ,函数
,函数 在
在 上单调递减,故
上单调递减,故 成立.
成立.
(ii) 当 时,由
时,由 ,因
,因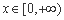 ,所以
,所以 ,
,
① 若 ,即
,即 时,在区间
时,在区间 上,
上, ,
,
则函数 在
在 上单调递增,
上单调递增, 在
在 上无最大值,当
上无最大值,当 时,
时,  ,此时不满足条件;
,此时不满足条件;
② 若 ,即
,即 时,函数
时,函数 在
在 上单调递减,
上单调递减,
在区间 上单调递增,同样
上单调递增,同样 在
在 上无最大值,当
上无最大值,当 时,
时,  ,不满足条件.
,不满足条件.
(iii) 当 时,由
时,由 ,∵
,∵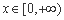 ,∴
,∴ ,
,
∴ ,故函数
,故函数 在
在 上单调递减,故
上单调递减,故 成立.
成立.
综上所述,实数a的取值范围是 .
.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 ),
), .
.

 )=
)= ,(k=1,2,3), 其中c为常数,则E
,(k=1,2,3), 其中c为常数,则E f(x)=
f(x)= 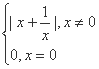 则关于x的方程
则关于x的方程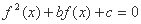 有5个不同实数解的充要条件是 ( )
有5个不同实数解的充要条件是 ( )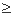 -2 且 c=0
-2 且 c=0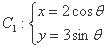 (
(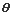 为参数),曲线
为参数),曲线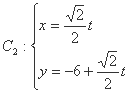 (t为参数),分别将曲线
(t为参数),分别将曲线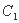 与曲线
与曲线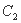 化为普通方程。(2)点P是曲线
化为普通方程。(2)点P是曲线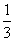 ,bn-1=27bn(n≥2且n∈N+),若an+logkbn为常数,则满足条件的k值( )
,bn-1=27bn(n≥2且n∈N+),若an+logkbn为常数,则满足条件的k值( )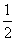 ,
,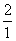 ,
,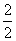 ,
,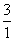 ,
,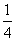 ,
,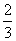 ,
,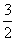 ,
,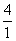 ,…,则
,…,则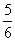 是数列中的( )
是数列中的( ) a12的值为( )
a12的值为( ) 则
则 的取值范围是( )
的取值范围是( )