题目内容
设数列{an}的前n项和为Sn,且Sn=(m+1)﹣man对于任意的正整数n都成立,其中m为常数,且m<﹣1.
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足: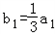 ,bn=f(bn﹣1)
,bn=f(bn﹣1)
(n≥2,n∈N),求证:数列{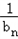 }是等差数列,并求数列{bnbn+1}的前n项和.
}是等差数列,并求数列{bnbn+1}的前n项和.
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足:
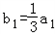 ,bn=f(bn﹣1)
,bn=f(bn﹣1)(n≥2,n∈N),求证:数列{
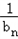 }是等差数列,并求数列{bnbn+1}的前n项和.
}是等差数列,并求数列{bnbn+1}的前n项和.解:(1)由已知Sn=(m+1)﹣man;Sn+1=(m+1)﹣man+1,相减,
得:an+1=man﹣man+1,即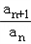 =
=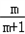 ,
,
所以{an}是等比数列
(2)当n=1时,a1=m+1﹣ma1,则a1=1,从而b1= ,
,
由(1)知q=f(m)=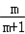 ,
,
所以bn=f(bn﹣1)=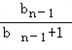 (n≥2)
(n≥2)
∴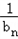 =1+
=1+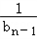 ,
,
∴数列{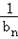 }是首项为
}是首项为 ,公差为1的等差数列
,公差为1的等差数列
∴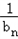 =3+(n﹣1)=n+2,
=3+(n﹣1)=n+2,
故:bn=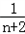 (n≥1),
(n≥1),
∴bnbn+1=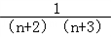 =
=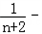
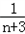 ;
;
∴数列{bnbn+1}的前n项和A=( ﹣
﹣ )+(
)+( ﹣
﹣ )+…+(
)+…+(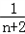 ﹣
﹣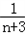 )=
)= ﹣
﹣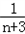 =
=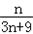 .
.
得:an+1=man﹣man+1,即
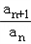 =
=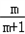 ,
,所以{an}是等比数列
(2)当n=1时,a1=m+1﹣ma1,则a1=1,从而b1=
 ,
,由(1)知q=f(m)=
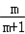 ,
,所以bn=f(bn﹣1)=
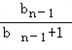 (n≥2)
(n≥2)∴
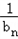 =1+
=1+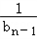 ,
,∴数列{
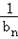 }是首项为
}是首项为 ,公差为1的等差数列
,公差为1的等差数列∴
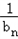 =3+(n﹣1)=n+2,
=3+(n﹣1)=n+2,故:bn=
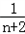 (n≥1),
(n≥1),∴bnbn+1=
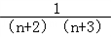 =
=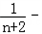
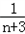 ;
;∴数列{bnbn+1}的前n项和A=(
 ﹣
﹣ )+(
)+( ﹣
﹣ )+…+(
)+…+(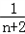 ﹣
﹣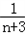 )=
)= ﹣
﹣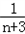 =
=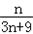 .
.
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目