题目内容
已知A(1,
)是离心率为
的椭圆E:
+
=1(a>b>0)上的一点,过A作两条直线交椭圆于B、C两点,若直线AB、AC的倾斜角互补.
(1)求椭圆E的方程;
(2)试证明直线BC的斜率为定值,并求出这个定值;
(3)△ABC的面积是否存在最大值?若存在,求出这个最大值?若不存在,说明理由.
| 2 |
| ||
| 2 |
| y2 |
| a2 |
| x2 |
| b2 |
(1)求椭圆E的方程;
(2)试证明直线BC的斜率为定值,并求出这个定值;
(3)△ABC的面积是否存在最大值?若存在,求出这个最大值?若不存在,说明理由.
分析:(1)利用A(1,
)是离心率为
的椭圆E:
+
=1(a>b>0)上的一点,建立方程,求出几何量,即可得到椭圆的标准方程;
(2)设出直线方程,代入椭圆方程,确定B,C的坐标,即可求出直线BC的斜率为定值;
(3)设出直线方程,代入椭圆方程,利用韦达定理,确定三角形的面积,利用基本不等式,即可求得结论.
| 2 |
| ||
| 2 |
| y2 |
| a2 |
| x2 |
| b2 |
(2)设出直线方程,代入椭圆方程,确定B,C的坐标,即可求出直线BC的斜率为定值;
(3)设出直线方程,代入椭圆方程,利用韦达定理,确定三角形的面积,利用基本不等式,即可求得结论.
解答:(1)解:∵椭圆的离心率为
,∴
=
,∴a2=2b2
∴椭圆方程为
+
=1
∵A(1,
)是椭圆上的点,
∴
+
=1
∴b2=2
∴椭圆方程为
+
=1;
(2)证明:设直线AB的方程为y-
=k(x-1),代入椭圆方程可得(k2+2)x2-2k(k-
)x+(k2-2
k-2)=0,∵x=1是方程的一个实根,
∴由韦达定理得,1+xB=
,故xB=
,
∴yB=k(xB-1)+
=
,
∴B(
,
),
∵AB、AC的倾斜角互补,故其斜率互为相反数,用-k代替k可得
C(
,
),∴kBC=
=
=
(3)解:设BC的方程为y=
x+m,由
可得4x2+2
mx+m2-4=0,
设方程的两根为x1,x2,于是|BC|=
•
=
,
又A(1,
)到直线BC的距离为d=
,
∴S△ABC=
•
•
=
•
≤
×4=
,
当且仅当m2=4时等号成立,故△ABC的面积的最大值为
.
| ||
| 2 |
| a2-b2 |
| a2 |
| 1 |
| 2 |
∴椭圆方程为
| y2 |
| 2b2 |
| x2 |
| b2 |
∵A(1,
| 2 |
∴
| 2 |
| 2b2 |
| 1 |
| b2 |
∴b2=2
∴椭圆方程为
| y2 |
| 4 |
| x2 |
| 2 |
(2)证明:设直线AB的方程为y-
| 2 |
| 2 |
| 2 |
∴由韦达定理得,1+xB=
2k(k-
| ||
| k2+2 |
k2-2
| ||
| k2+2 |
∴yB=k(xB-1)+
| 2 |
-
| ||||
| k2+2 |
∴B(
k2-2
| ||
| k2+2 |
-
| ||||
| k2+2 |
∵AB、AC的倾斜角互补,故其斜率互为相反数,用-k代替k可得
C(
k2+2
| ||
| k2+2 |
-
| ||||
| k2+2 |
| yB-yC |
| xB-xC |
| 8k | ||
4
|
| 2 |
(3)解:设BC的方程为y=
| 2 |
|
| 2 |
设方程的两根为x1,x2,于是|BC|=
| 3 |
| (x1+x2)2-4x1x2 |
|
又A(1,
| 2 |
| |m| | ||
|
∴S△ABC=
| 1 |
| 2 |
|
| |m| | ||
|
| ||
| 4 |
| m2(8-m2) |
| ||
| 4 |
| 2 |
当且仅当m2=4时等号成立,故△ABC的面积的最大值为
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
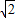 )是离心率为
)是离心率为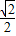 的椭圆E:
的椭圆E: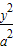 +
+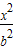 =1(a>b>0)上的一点,过A作两条直线交椭圆于B、C两点,若直线AB、AC的倾斜角互补.
=1(a>b>0)上的一点,过A作两条直线交椭圆于B、C两点,若直线AB、AC的倾斜角互补.