题目内容
 在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则点P到BC的距离是
在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则点P到BC的距离是
- A.

- B.2

- C.3

- D.4

D
分析:过A作AD⊥BC于D,连接PD,说明BC⊥PD,点P到BC的距离是PD,在直角三角形PAD中求出PD即可.
解答:过A作AD⊥BC于D,连接PD,
因为AB=AC=5,BC=6,,所以BD=DC=3,
又∵PA⊥平面ABC,PA∩AD=A,
∴BC⊥PD,
∴点P到BC的距离是PD,
在△ADC中,AC=5,DC=3,∴AD=4,
在Rt△PAD中,PD=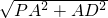 =
=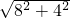 =
=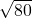 =4
=4 .
.
故选D.
点评:本题是中档题,考查空间点到直线的距离,作出点到直线的距离是解题的关键,考查空间想象能力,计算能力.
分析:过A作AD⊥BC于D,连接PD,说明BC⊥PD,点P到BC的距离是PD,在直角三角形PAD中求出PD即可.
解答:过A作AD⊥BC于D,连接PD,
因为AB=AC=5,BC=6,,所以BD=DC=3,
又∵PA⊥平面ABC,PA∩AD=A,
∴BC⊥PD,
∴点P到BC的距离是PD,
在△ADC中,AC=5,DC=3,∴AD=4,

在Rt△PAD中,PD=
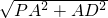 =
=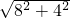 =
=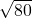 =4
=4 .
.故选D.
点评:本题是中档题,考查空间点到直线的距离,作出点到直线的距离是解题的关键,考查空间想象能力,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目