题目内容
已知数列{an}满足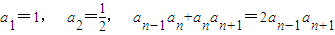 .
.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}的前n项和为
 ,试求数列
,试求数列 的前n项和Tn;
的前n项和Tn;(Ⅲ)记数列
 的前n项积为
的前n项积为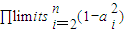 ,试证明:
,试证明: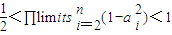 .
.
【答案】分析:(I)由an-1an+anan+1=2an-1an+1,两边同除以anan-1an+1即可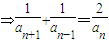 .而
.而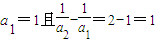 ,故
,故 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
(II)利用bn=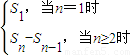 即可得到bn,可得
即可得到bn,可得 =
= ,利用“错位相减法”即可得到Tn;
,利用“错位相减法”即可得到Tn;
(III)因为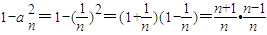 .利用“累乘求积”即可得出
.利用“累乘求积”即可得出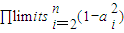 =
= .进而即可证明.
.进而即可证明.
解答:解:(Ⅰ)由
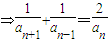
 .
.
而 ,
,
因此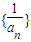 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.
从而 .
.
(Ⅱ)当n=1时, .
.
当n≥2时, .
.
而b1也符合上式,故 ,从而:
,从而: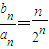 .
.
所以 .
.
将上面两式相减,可得: .
.
(Ⅲ)因为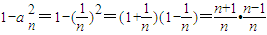 .
.
故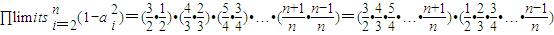
 .
.
由于n≥2,n∈N*,故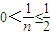 ,从而
,从而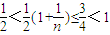 ,即
,即 .
.
点评:本题考查数列的递推公式的处理、等差数列的通项公式和前n项和求通项以及“错位相减法”、“累乘求积”等基础知识,突出考查了学生变形的能力,化归与转化的思想以及创新意识,是一道十分重视基础但又有比较好区分度的中等题.
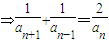 .而
.而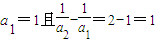 ,故
,故 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.(II)利用bn=
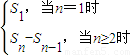 即可得到bn,可得
即可得到bn,可得 =
= ,利用“错位相减法”即可得到Tn;
,利用“错位相减法”即可得到Tn;(III)因为
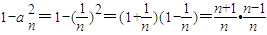 .利用“累乘求积”即可得出
.利用“累乘求积”即可得出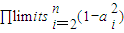 =
= .进而即可证明.
.进而即可证明.解答:解:(Ⅰ)由

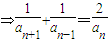
 .
.而
 ,
,因此
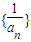 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列.从而
 .
.(Ⅱ)当n=1时,
 .
.当n≥2时,
 .
.而b1也符合上式,故
 ,从而:
,从而: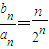 .
.所以
 .
.将上面两式相减,可得:
 .
.(Ⅲ)因为
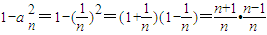 .
.故
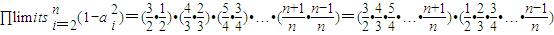
 .
.由于n≥2,n∈N*,故
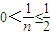 ,从而
,从而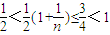 ,即
,即 .
.点评:本题考查数列的递推公式的处理、等差数列的通项公式和前n项和求通项以及“错位相减法”、“累乘求积”等基础知识,突出考查了学生变形的能力,化归与转化的思想以及创新意识,是一道十分重视基础但又有比较好区分度的中等题.

练习册系列答案
相关题目