题目内容
7．已知A，B，C三点不在同一条直线上，O是平面ABC内一定点，P是△ABC内的一动点，若$\overrightarrow{OP}-\overrightarrow{OA}=λ（\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}）$，λ∈[0，+∞），则直线AP一定过△ABC的（ ）| A． | 重心 | B． | 垂心 | C． | 外心 | D． | 内心 |
分析 通过画出草图，数形结合即得结论．
解答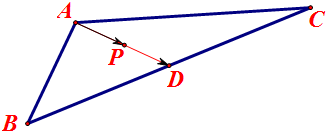 
解：如图，取BC的中点P并连结AD，
则$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$=$\overrightarrow{AD}$、$\overrightarrow{OP}$-$\overrightarrow{OA}$=$\overrightarrow{AP}$，
∵$\overrightarrow{OP}-\overrightarrow{OA}=λ（\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}）$，λ∈[0，+∞），
∴$\overrightarrow{AP}$=λ$\overrightarrow{AD}$，即A、P、D三点共线，
又∵AD为BC边上的中线，
∴直线AP一定过△ABC的重心，
故选：A．
点评 本题考查平面向量的线性运算性质及其几何意义，注意解题方法的积累，属于基础题．
练习册系列答案
相关题目
18．在△ABC中，a=3，b=5，c=7，那么这个三角形的最大角是（ ）
| A． | 135° | B． | 150° | C． | 90° | D． | 120° |
19．圆x2+y2=1在伸缩变换$\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}\right.$的作用下，所得方程是（ ）
| A． | 4x′2+9y′2=1 | B． | $\frac{{{{x'}^2}}}{2}+\frac{{{{y'}^2}}}{3}=1$ | C． | $\frac{{{{x'}^2}}}{9}+\frac{{{{y'}^2}}}{4}=1$ | D． | $\frac{{{{x'}^2}}}{4}+\frac{{{{y'}^2}}}{9}=1$ |