题目内容
5.关于x的一元二次方程x2-2ax+a+2=0在(1,3)内有两个不同实根,则a取值范围为(2,$\frac{11}{5}$).分析 设f(x)=x2-2ax+a+2,则f(x)在(1,3)上有两个不同实根,所以f(1)>0,f(3)>0,fmin(x)<0,解不等式组得出答案.
解答 解:设f(x)=x2-2ax+a+2,
则f(x)在(1,3)上有两个不同实根,
∴$\left\{\begin{array}{l}{f(1)>0}\\{f(3)>0}\\{{f}_{min}(x)<0}\end{array}\right.$,即$\left\{\begin{array}{l}{1-2a+a+2>0}\\{9-6a+a+2>0}\\{\frac{4(a+2)-4{a}^{2}}{4}<0}\end{array}\right.$,
解得2<a<$\frac{11}{5}$.
故答案为(2,$\frac{11}{5}$).
点评 本题考查了二次函数的零点与根的关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若以双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右焦点和点(1,$\sqrt{2}$)为顶点的三角形为直角三角形,则b等于( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
16.设椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$的焦点为F1、F2,直线L过点F1,且与椭圆相交于A,B两点,则△ABF2的周长为( )
| A. | 9 | B. | 16 | C. | 20 | D. | 25 |
20.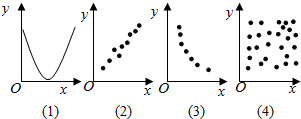 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )
 如图,两个变量具有相关关系的图是( )
如图,两个变量具有相关关系的图是( )| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (2)(3) |
10.已知$f(\sqrt{x}-1)=x-2\sqrt{x}$,且f(a)=8,则实数a的值是( )
| A. | ±3 | B. | 16 | C. | -3 | D. | 3 |