题目内容
已知函数f(x)= sin2x-cos2x-
sin2x-cos2x- ,x∈R,
,x∈R,
(1)求函数f(x)的最小值和最小正周期;
(2)求函数在[- ,
, ]上的最大值和最小值.
]上的最大值和最小值.
解:(1)f(x)= sin2x-cos2x-
sin2x-cos2x- =
= sin2x-
sin2x-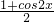 -
- =sin(2x-
=sin(2x- )-1
)-1
∴函数f(x)的最小值是-2和最小正周期为 ;
;
(2)∵x∈[- ,
, ],
],
∴(2x- )∈
)∈
∴sin(2x- )∈
)∈
∴函数在[- ,
, ]上的最大值为
]上的最大值为 和最小值为-2.
和最小值为-2.
分析:(1)利用三角恒等变换公式,化简函数,即可求出函数f(x)的最小值和最小正周期;
(2)根据x∈[- ,
, ],可得(2x-
],可得(2x- )∈
)∈ ,从而可求sin(2x-
,从而可求sin(2x- )∈
)∈ ,进而可求函数在[-
,进而可求函数在[- ,
, ]上的最大值和最小值.
]上的最大值和最小值.
点评:本题考查三角恒等变换,考查函数的性质,考查整体思维的思想,属于中档题.
 sin2x-cos2x-
sin2x-cos2x- =
= sin2x-
sin2x-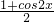 -
- =sin(2x-
=sin(2x- )-1
)-1∴函数f(x)的最小值是-2和最小正周期为
 ;
;(2)∵x∈[-
 ,
, ],
],∴(2x-
 )∈
)∈
∴sin(2x-
 )∈
)∈
∴函数在[-
 ,
, ]上的最大值为
]上的最大值为 和最小值为-2.
和最小值为-2.分析:(1)利用三角恒等变换公式,化简函数,即可求出函数f(x)的最小值和最小正周期;
(2)根据x∈[-
 ,
, ],可得(2x-
],可得(2x- )∈
)∈ ,从而可求sin(2x-
,从而可求sin(2x- )∈
)∈ ,进而可求函数在[-
,进而可求函数在[- ,
, ]上的最大值和最小值.
]上的最大值和最小值.点评:本题考查三角恒等变换,考查函数的性质,考查整体思维的思想,属于中档题.

练习册系列答案
相关题目
