题目内容
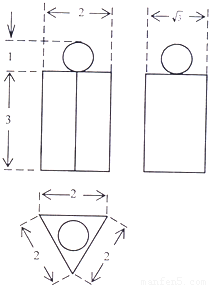
 如图,一个几何体三视图的正视图和侧视图为边长为2锐角60°的菱形,俯视图为正方形,则此几何体的内切球表面积为( )
如图,一个几何体三视图的正视图和侧视图为边长为2锐角60°的菱形,俯视图为正方形,则此几何体的内切球表面积为( )| A、8π | B、4π | C、3π | D、2π |
分析:由题意可知,该几何体的内切球的球心即为该几何体的中心,进而可求此几何体的内切球的半径,即可得到此几何体的内切球表面积.
解答:解:由于此几何体三视图的正视图和侧视图为边长为2锐角60°的菱形,俯视图为正方形,
则该几何体的内切球的球心即为该几何体的中心,即是正方形的中心.
由此几何体三视图可知,几何体每个面的三边长分别为
,
,2,
设此几何体的内切球的半径为r,则由体积相等得到:4×
×
×2×2×r=
×2×2×
解得r=
,则此几何体的内切球表面积为4π×(
)2=3π
故答案为 C.
则该几何体的内切球的球心即为该几何体的中心,即是正方形的中心.
由此几何体三视图可知,几何体每个面的三边长分别为
| 5 |
| 5 |
设此几何体的内切球的半径为r,则由体积相等得到:4×
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
解得r=
| ||
| 2 |
| ||
| 2 |
故答案为 C.
点评:本题考查由几何体的三视图求其内切球的表面积问题,属于基础题.

练习册系列答案
相关题目
 (2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )
(2012•马鞍山二模)如图是一个几何体的三视,则它的表面为( )
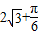
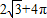

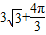






 π
π π
π