题目内容
如图,正方形ABCD和ABEF的边长均为1,且它们所在的平面互相垂直,G为BC的中点.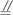
(1)求点G到平面ADE的距离;
(2)(理)求直线AD与平面DEG所成的角;
(文)求二面角EGDA的正切值.
解:(1)∵BC∥AD,AD![]() 面ADE,∴点G到面ADE的距离即点B到面ADE的距离.
面ADE,∴点G到面ADE的距离即点B到面ADE的距离.
连结BF交AE于H,则BF⊥AE,又BF⊥AD,∴BH即为点B到面ADE的距离.
在Rt△ABE中,BH=![]() .∴点G到面ADE的距离为
.∴点G到面ADE的距离为![]() .
.
(2)(理)设DE中点为O,连结OG、OH,则OH![]()
![]() AD,BG
AD,BG![]()
![]() AD.
AD.

∴四边形BHOG为平行四边形.
∴GO∥BH.由(1),BH⊥面ADE,∴GO⊥面ADE.
又OG![]() 面DEG,∴面DEG⊥面ADE.∴过点A作AM⊥DE于M,则AM⊥面DEG.∴∠ADE为直线AD与面DEG所成的角.
面DEG,∴面DEG⊥面ADE.∴过点A作AM⊥DE于M,则AM⊥面DEG.∴∠ADE为直线AD与面DEG所成的角.
在Rt△ADE中,tan∠ADE=![]() .∴∠ADE=arctan
.∴∠ADE=arctan![]() .∴AD与平面DEG所成的角为arctan2.
.∴AD与平面DEG所成的角为arctan2.
(文)过点B作BN⊥DG于点N,连结EN,由三垂线定理,知EN⊥DN.
∴∠ENB为二面角EGDA的平面角.
在Rt△BNG中,sin∠BGN=sin∠DGC=![]() ,∴BN=BG·sin∠BGN=
,∴BN=BG·sin∠BGN=![]() ·
·![]() =
=![]() .
.
则在Rt△EBN中,tan∠ENB=![]() .
.
∴二面角EBDA的正切值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ.
已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ. 如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且
如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且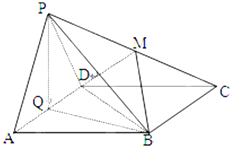 如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.