Question

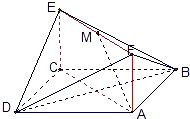
如图，已知正方形ABCD的边长为4，CG⊥平面ABCD，CG＝2，E、F分别是AB、AD的中点，求点B到平面GEF的距离．

Answer 1

答案：
解析：

解：连结BD、AC，EF和BD分别交AC于H、O，连结GH，作OK⊥GH于点K． 　　∵ABCD为正方形，E、F分别为AB、AD的中点，∴EF∥BD，H为AO的中点． 　　∵BD∥EF，BD平面GFE，∴BD∥平面GFE． 　　∴BD与平面GFE的距离就是O点到平面EFG的距离． 　　∵BD⊥AC，∴EF⊥AC．∵GC⊥面ABCD，∴GC⊥EF． 　　∵GC∩AC＝C，∴EF⊥平面GCH．∵OK平面GCH，∴EF⊥OK． 　　又∵OK⊥GH，GH∩EF＝H，∴OK⊥平面GEF，即OK的长就是点B到平面GEF的距离． 　　∵正方形的边长为4，CG＝2，∴AC＝，HO＝，HC＝． 　　在Rt△HCG中，HG＝． 在Rt△GCH中，OK＝．

提示：

本题是求平面外一点到平面的距离，可用转移法将该点到平面的距离转化为求另一点到该平面的距离．为此要寻找过点B与平面GEF平行的直线，因为与平面平行的直线上所有点到平面的距离相等．