题目内容
已知函数f(x)=(-x2+ax+b)e-x,a∈R
(1)若b=-a,求y=f(x)的单调区间;
(2)若b=0,且f(x)在(-1,1)上单调递减,求a的取值范围.
解:(1)当b=-a时,函数f(x)=(-x2+ax-a)e-x,∴f′(x)=[x2-(2+a)x+2a]e-x=(x-a)(x-2)e-x,令f′(x)=0,则x=2或a.
①当a=2时,f′(x)=(x-2)2e-x≥0,因此f(x)在R上单调递增;
②当a>2时,如表所示,函数在区间(-∞,2),(a,+∞)上单调递增;在区间(2,a)上单调递减;
③同理:当a<2时,函数在区间(-∞,a),(2,+∞)上单调递增;在区间(a,2)上单调递减.
(2)b=0,f(x)=(-x2+ax)e-x,∴f′(x)=[x2-(a+2)x+a]e-x.
∵f(x)在(-1,1)上单调递减,∴f′(x)≤0,∴x2-(a+2)x+a≤0在(-1,1)上单调递减,
∴ ,解得
,解得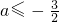 .
.
因此a的取值范围为 .
.
分析:(1)先解出f′(x)=0,通过对a分类讨论即可得出其单调区间;
(2)f(x)在(-1,1)上单调递减?f′(x)≤0,解出即可.
点评:熟练掌握利用对数研究函数的单调性和极值及分类讨论的思想方法是解题的关键.
①当a=2时,f′(x)=(x-2)2e-x≥0,因此f(x)在R上单调递增;

②当a>2时,如表所示,函数在区间(-∞,2),(a,+∞)上单调递增;在区间(2,a)上单调递减;
③同理:当a<2时,函数在区间(-∞,a),(2,+∞)上单调递增;在区间(a,2)上单调递减.
(2)b=0,f(x)=(-x2+ax)e-x,∴f′(x)=[x2-(a+2)x+a]e-x.
∵f(x)在(-1,1)上单调递减,∴f′(x)≤0,∴x2-(a+2)x+a≤0在(-1,1)上单调递减,
∴
 ,解得
,解得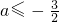 .
.因此a的取值范围为
 .
.分析:(1)先解出f′(x)=0,通过对a分类讨论即可得出其单调区间;
(2)f(x)在(-1,1)上单调递减?f′(x)≤0,解出即可.
点评:熟练掌握利用对数研究函数的单调性和极值及分类讨论的思想方法是解题的关键.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|