题目内容
在等差数列{an}中,a1=-2012,其前n项的和为Sn.若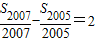 ,则S2012=( )
,则S2012=( )A.-2007
B.-2012
C.2007
D.2008
【答案】分析:由等差数列{an}的前n项和公式Sn=na1+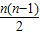 d可得{
d可得{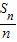 }为等差数列,由题意可求得d=2,从而可求得S2012的值.
}为等差数列,由题意可求得d=2,从而可求得S2012的值.
解答:解:∵数列{an}为等差数列,设其公差为d,则其前n项和为Sn=na1+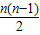 d,
d,
∴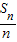 =na1+
=na1+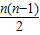 d,∴
d,∴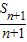 -
-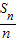 =
=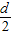 ,
,
∴{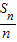 }为公差是
}为公差是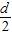 的等差数列,
的等差数列,
∴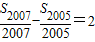 ×
×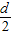 =2,可得d=2,
=2,可得d=2,
∵数列{an}为等差数列,a1=-2012,
S2012=2012a1+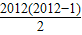 ×2=2012×(-2012)+2012(2012-1)=-2012,
×2=2012×(-2012)+2012(2012-1)=-2012,
故选B;
点评:本题考查等差数列的求和,分析得到{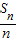 }公差是
}公差是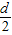 的等差数列是关键,也是难点所在,考查分析问题、解决问题的能力,属于中档题.
的等差数列是关键,也是难点所在,考查分析问题、解决问题的能力,属于中档题.
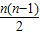 d可得{
d可得{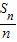 }为等差数列,由题意可求得d=2,从而可求得S2012的值.
}为等差数列,由题意可求得d=2,从而可求得S2012的值.解答:解:∵数列{an}为等差数列,设其公差为d,则其前n项和为Sn=na1+
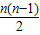 d,
d,∴
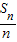 =na1+
=na1+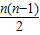 d,∴
d,∴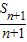 -
-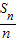 =
=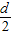 ,
,∴{
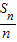 }为公差是
}为公差是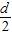 的等差数列,
的等差数列,∴
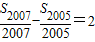 ×
×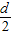 =2,可得d=2,
=2,可得d=2,∵数列{an}为等差数列,a1=-2012,
S2012=2012a1+
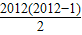 ×2=2012×(-2012)+2012(2012-1)=-2012,
×2=2012×(-2012)+2012(2012-1)=-2012,故选B;
点评:本题考查等差数列的求和,分析得到{
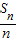 }公差是
}公差是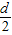 的等差数列是关键,也是难点所在,考查分析问题、解决问题的能力,属于中档题.
的等差数列是关键,也是难点所在,考查分析问题、解决问题的能力,属于中档题. 
练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目