题目内容
已知函数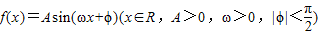 的部分图象如图所示,则f(-1)= .
的部分图象如图所示,则f(-1)= .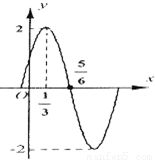
【答案】分析:由图象可得A=2,由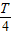 可得ω=π,代入点(
可得ω=π,代入点( ,0)可得ϕ的值,进而可得函数解析式,代入-1可得答案.
,0)可得ϕ的值,进而可得函数解析式,代入-1可得答案.
解答:解:由图象可得A=2,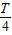 =
=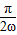 =
=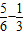 ,解得ω=π,
,解得ω=π,
故函数的解析式为:f(x)=2sin(πx+ϕ),代入点( ,0)可得
,0)可得
0=2sin(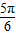 +ϕ),解得ϕ=
+ϕ),解得ϕ=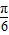 ,
,
故函数的解析式为:f(x)=2sin(πx+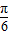 ),
),
故f(-1)=2sin(-π+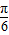 )=-2sin
)=-2sin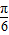 =-1,
=-1,
故答案为:-1
点评:本题考查由图象确定函数f(x)=Asin(ωx+ϕ)的解析式,属基础题.
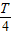 可得ω=π,代入点(
可得ω=π,代入点( ,0)可得ϕ的值,进而可得函数解析式,代入-1可得答案.
,0)可得ϕ的值,进而可得函数解析式,代入-1可得答案.解答:解:由图象可得A=2,
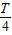 =
=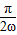 =
=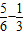 ,解得ω=π,
,解得ω=π,故函数的解析式为:f(x)=2sin(πx+ϕ),代入点(
 ,0)可得
,0)可得0=2sin(
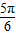 +ϕ),解得ϕ=
+ϕ),解得ϕ=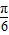 ,
,故函数的解析式为:f(x)=2sin(πx+
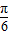 ),
),故f(-1)=2sin(-π+
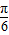 )=-2sin
)=-2sin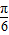 =-1,
=-1,故答案为:-1
点评:本题考查由图象确定函数f(x)=Asin(ωx+ϕ)的解析式,属基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 的部分图象如右图所示,设
的部分图象如右图所示,设 是图象的最高点,
是图象的最高点, 是图象与
是图象与 轴的交点,则
轴的交点,则 ( )
( )
 B.
B.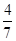 C.
C. D.
D.

 的部分图象如图所示.
的部分图象如图所示. ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由.
 的部分图象如图所示.
的部分图象如图所示. ,求函数f(x)的值域.
,求函数f(x)的值域.
 的部分图象如图所示,则
的部分图象如图所示,则 的解析式是 ( )
的解析式是 ( ) B.
B.
 D.
D.


 的部分图象如右图所示,则
的部分图象如右图所示,则 的值为________.
的值为________.