题目内容
(.(本小题满分12分)
已知点A,B的坐标分别是(0,–1),(0,1),直线AM,BM相交于点M,且它们的斜率之积为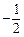 .
.
(1) 求点M的轨迹C的方程;
(2) 若过点D(2,0)的直线l与(1)中的轨迹C交于不同的两点E、F (E在D、F之间),试求
(E在D、F之间),试求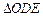 与
与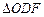 面积之比的取值范围(O为坐标原点).
面积之比的取值范围(O为坐标原点).
解:(1) 设点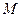 的坐标为
的坐标为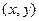 ,
,
∵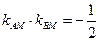 ,∴
,∴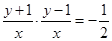 .
.
整理,得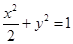 (
(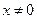 ),这就是动点M的轨迹方程.··········· 4分
),这就是动点M的轨迹方程.··········· 4分
(2) 解法一:由题意知直线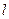 的斜率存在,设
的斜率存在,设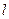 的方程
的方程 为
为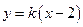 (
(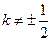 )①
)①
将①代入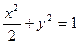 ,得
,得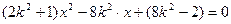 (*)
(*)
由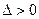 ,解得
,解得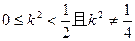
由(*)式得
设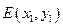 ,
,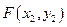 ,则
,则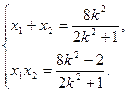 ②
②
令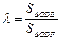 ,则
,则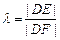 ,即
,即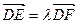 ,
,
即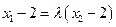 ,且
,且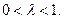
由②得,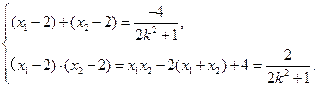
即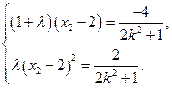
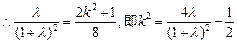 .
. 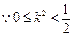 且
且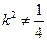
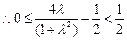 且
且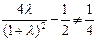 .
.
解得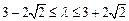 且
且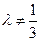
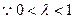 ,
,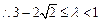 且
且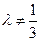 .
.
∴△OBE与△OBF面积之比的取值范围是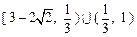 .………………12分
.………………12分
解法二:设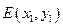 ,
,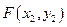 ,则
,则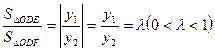
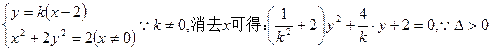 可得:
可得: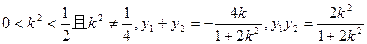 ,将
,将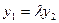 代入可得:
代入可得: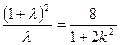
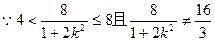
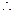
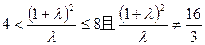
解得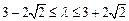 且
且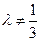
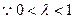 ,
,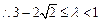 且
且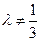 .………12分
.………12分
解析

练习册系列答案
相关题目
 内的随机点,求函数
内的随机点,求函数