题目内容
已知函数
(Ⅰ)求曲线y=f(x)在(1,11)处的切线方程;(Ⅱ)求函数的单调区间
(Ⅲ)求函数在[-2,2]上的最值。
【答案】
(Ⅰ)12x-y-11=0(Ⅱ) (Ⅲ)x=-1,
(Ⅲ)x=-1, .当
.当
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)因为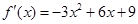 ,所以切线的斜率为
,所以切线的斜率为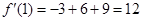
所以切线方程y-1=12(x-1)即 12x-y-11=0
(2)令令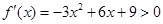 得
得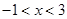 所以函数f(x)的单调增区间为(-1,3)
所以函数f(x)的单调增区间为(-1,3)
令 得x<-1或x>3所以函数f(x)的单调减区间为
得x<-1或x>3所以函数f(x)的单调减区间为 ,得到结论。
,得到结论。
(3)因为在(-2,-1)上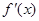 <0,在(-1,2)
<0,在(-1,2)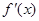 >0所以f(x)在(-2,-1)单调递减,在(-1,2)上单调递增故得到最值。
>0所以f(x)在(-2,-1)单调递减,在(-1,2)上单调递增故得到最值。
解:(Ⅰ)因为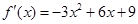 ,所以切线的斜率为
,所以切线的斜率为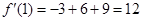
所以切线方程y-1=12(x-1)即 12x-y-11=0
(Ⅱ)令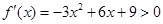 得
得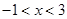 所以函数f(x)的单调增区间为(-1,3)
所以函数f(x)的单调增区间为(-1,3)
令 得x<-1或x>3所以函数f(x)的单调减区间为
得x<-1或x>3所以函数f(x)的单调减区间为
(Ⅲ)因为在(-2,-1)上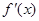 <0,在(-1,2)
<0,在(-1,2)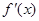 >0所以f(x)在(-2,-1)单调递减,在(-1,2)上单调递增。所以x=-1,
>0所以f(x)在(-2,-1)单调递减,在(-1,2)上单调递增。所以x=-1, .当
.当

练习册系列答案
相关题目
 -2lnx、
-2lnx、 -2lnx、
-2lnx、 -2lnx、
-2lnx、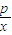 -2lnx、
-2lnx、