题目内容
已知函数 ,a∈R且a≠0.
,a∈R且a≠0.
(1)若对?x∈R,都有f(x)≤0,求a的取值范围;
(2)若a≥2,且?x∈R,使得f(x)≤0,求a的取值范围.
解:(1) .
.
令t=sinx(-1≤t≤1),则 ,
,
对任意x∈R,f(x)≤0恒成立的充要条件是
解得a的取值范围为(0,1];
(2)因为a≥2,所以 ,g(t)在[-1,1]上递增,
,g(t)在[-1,1]上递增,
所以 ,
,
因此 .
.
于是,存在x∈R,使得f(x)≤0的充要条件是 ,解得0<a≤3,
,解得0<a≤3,
故a的取值范围是[2,3].
分析:(1)f(x)可变为: .令t=sinx(-1≤t≤1),则
.令t=sinx(-1≤t≤1),则 ,则任意x∈R,f(x)≤0恒成立?g(-1)≤0,g(1)≤0,解出即可;
,则任意x∈R,f(x)≤0恒成立?g(-1)≤0,g(1)≤0,解出即可;
(2)x∈R,使得f(x)≤0,等价于f(x)min=g(t)min≤0,当a≥2时,由g(t)在[-1,1]上的单调性易求其最小值;
点评:本题考查函数恒成立问题,函数恒成立问题往往转化为函数最值问题解决,体现了转化思想,注意区分“恒成立”与“能成立”的区别.
 .
.令t=sinx(-1≤t≤1),则
 ,
,对任意x∈R,f(x)≤0恒成立的充要条件是

解得a的取值范围为(0,1];
(2)因为a≥2,所以
 ,g(t)在[-1,1]上递增,
,g(t)在[-1,1]上递增,所以
 ,
,因此
 .
.于是,存在x∈R,使得f(x)≤0的充要条件是
 ,解得0<a≤3,
,解得0<a≤3,故a的取值范围是[2,3].
分析:(1)f(x)可变为:
 .令t=sinx(-1≤t≤1),则
.令t=sinx(-1≤t≤1),则 ,则任意x∈R,f(x)≤0恒成立?g(-1)≤0,g(1)≤0,解出即可;
,则任意x∈R,f(x)≤0恒成立?g(-1)≤0,g(1)≤0,解出即可;(2)x∈R,使得f(x)≤0,等价于f(x)min=g(t)min≤0,当a≥2时,由g(t)在[-1,1]上的单调性易求其最小值;
点评:本题考查函数恒成立问题,函数恒成立问题往往转化为函数最值问题解决,体现了转化思想,注意区分“恒成立”与“能成立”的区别.

练习册系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.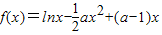 (a∈R且a≠0).
(a∈R且a≠0).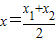 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.