题目内容
已知a>0,0≤x<2π,函数y=cos2x-asinx+b的最大值为0,最小值为-4,试求a和b的值,并求出使y取得最大值和最小值的x的值.
解析:y=cos2x-asinx+b
=1-sin2x-asinx+b=-sin2x-asinx+1+b.
令sinx=t,由于x∈[0,2π),
∴t∈[-1,1],则y=-t2-at+1+b=-(t2+at+![]() )+1+b+
)+1+b+![]() =-(t+a2)2+1+b+
=-(t+a2)2+1+b+![]() .
.
(1)当-a2∈[-1,1]时,即0<a≤2时,由图1知ymax=1+b+![]() ,ymin=-1-a+1+b=b-a.由条件得:
,ymin=-1-a+1+b=b-a.由条件得:
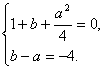
解得a=2或a=-6(舍去),
b=a-4=2-4=-2.
此时y=-t2-2t-1=-(t+1)2,当t=-1时,y取到最大值,且ymax=0.
此时x=![]() ,当t=1时.y取到最小值,且ymin=-4,此时x=
,当t=1时.y取到最小值,且ymin=-4,此时x=![]() .
.
(2)当![]() <-1即a>2时,由图2知y=-t2-at+1+b在[-1,1]上单调递减,此时ymax=-1+a+1+b=a+b,ymin=-1-a+1+b=b-a.
<-1即a>2时,由图2知y=-t2-at+1+b在[-1,1]上单调递减,此时ymax=-1+a+1+b=a+b,ymin=-1-a+1+b=b-a.
由条件得:![]()
解得:b=-2,a=2,由于a>2,所以该情况舍去.
综述:a=2,b=-2,y取到最大值时x的值为![]() ;y取到最小值时x的值为
;y取到最小值时x的值为![]() .
.
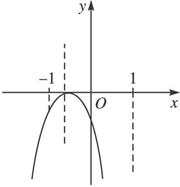
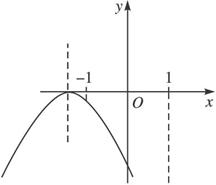
图1 图2

练习册系列答案
相关题目
 sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=
sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x= 是函数f(x)图象的一条对称轴,
是函数f(x)图象的一条对称轴,
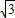 sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=
sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=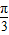 是函数f(x)图象的一条对称轴,
是函数f(x)图象的一条对称轴,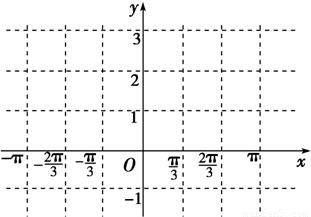
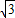 sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=
sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=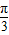 是函数f(x)图象的一条对称轴,
是函数f(x)图象的一条对称轴,
 sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x=
sinωx)(其中0<ω<1),函数f(x)=a•b,若直线x= 是函数f(x)图象的一条对称轴,
是函数f(x)图象的一条对称轴,