题目内容
在等差数列{an}中,已知a3=8,a9=24,求a6,a12以及S11.
解:在等差数列{an}中,由a3=8,a9=24,
∴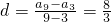 ,
,
∴a6=a3+3d=16,a12=a9+3d=32.
∴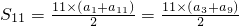 =
=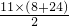 =176.
=176.
分析:题目给出的数列是等差数列,根据等差数列的定义,结合a3=8,a9=24可求等差数列的公差,则a6,a12可求,然后运用等差数列的前n项和公式,结合等差数列的性质把a1+a11转化成a3+a9可求s11.
点评:本题考查了等差数列的通项公式,考查了等差数列的定义及性质,运用了通项公式an=am+(n-m)d及性质am+an=ap+aq(m,n,p,q∈N*,且m+n=p+q),此题也可以设出首项和公差,利用通性通法求解,是基础题.
∴
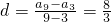 ,
,∴a6=a3+3d=16,a12=a9+3d=32.
∴
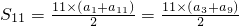 =
=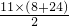 =176.
=176.分析:题目给出的数列是等差数列,根据等差数列的定义,结合a3=8,a9=24可求等差数列的公差,则a6,a12可求,然后运用等差数列的前n项和公式,结合等差数列的性质把a1+a11转化成a3+a9可求s11.
点评:本题考查了等差数列的通项公式,考查了等差数列的定义及性质,运用了通项公式an=am+(n-m)d及性质am+an=ap+aq(m,n,p,q∈N*,且m+n=p+q),此题也可以设出首项和公差,利用通性通法求解,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目