题目内容
已知函数f(x)=2sinx·(sinx+cosx).(1)求函数f(x)的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数y=f(x)在区间［-
,
］上的图象.
剖析:欲画f(x)的图象求f(x)的周期和最大值,需把f(x)化成一个角的一个三角函数的形式.
解:(1)f(x)=2sin2x+2sinxcosx=1-cos2x+sin2x=1+sin(2x-
),
∴f(x)的最小正周期为π,最大值为1+
.
(2)由(1)知,
x | - | - |
|
|
|
y | 1 | 1- | 1 | 1+ | 1 |
故函数y=f(x)在区间［-
,
］上的图象如下:
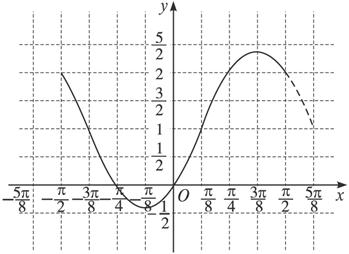
讲评:本题考查了三角函数的图象和性质,解决(2)的关键是利用“五点法”作图时,五个点的恰当选择.
练习册系列答案
相关题目