题目内容
已知抛物线y2=2px(p>0),过点E(m,0)(m≠0)的直线交抛物线于点M、N,交y轴于点P,若 ,则λ+μ=
,则λ+μ=
- A.1
- B.

- C.-1
- D.-2
C
分析:分别设M,N,P的坐标为(x1,y1),(x2,y2),(x0,y0),由 ,可得到x1,x2,y1,y2,再由直线MN的表达式,可用y来表示x,然后带到抛物线表达式中,根据韦达定理,求出y1,y2的积、和,分别等于之前算出的y1,y2的积、和.从而得出λ+μ=-1.
,可得到x1,x2,y1,y2,再由直线MN的表达式,可用y来表示x,然后带到抛物线表达式中,根据韦达定理,求出y1,y2的积、和,分别等于之前算出的y1,y2的积、和.从而得出λ+μ=-1.
解答:分别设M,N,P的坐标为(x1,y1),(x2,y2),(x0,y0),
∵ ,
,
∴ ,可得到x1,x2,y1,y2,
,可得到x1,x2,y1,y2,
直线MN的方程为: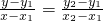 ,可用y来表示x,
,可用y来表示x,
然后带到抛物线表达式中,
根据韦达定理,求出y1,y2的积、和,分别等于之前算出的y1,y2的积、和.从而得出λ+μ=-1.
故选C.
点评:本题考查抛物线的性质和应用,解题时要注意向量和直线方程和合理运用.
分析:分别设M,N,P的坐标为(x1,y1),(x2,y2),(x0,y0),由
 ,可得到x1,x2,y1,y2,再由直线MN的表达式,可用y来表示x,然后带到抛物线表达式中,根据韦达定理,求出y1,y2的积、和,分别等于之前算出的y1,y2的积、和.从而得出λ+μ=-1.
,可得到x1,x2,y1,y2,再由直线MN的表达式,可用y来表示x,然后带到抛物线表达式中,根据韦达定理,求出y1,y2的积、和,分别等于之前算出的y1,y2的积、和.从而得出λ+μ=-1.解答:分别设M,N,P的坐标为(x1,y1),(x2,y2),(x0,y0),
∵
 ,
,∴
 ,可得到x1,x2,y1,y2,
,可得到x1,x2,y1,y2,直线MN的方程为:
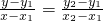 ,可用y来表示x,
,可用y来表示x,然后带到抛物线表达式中,
根据韦达定理,求出y1,y2的积、和,分别等于之前算出的y1,y2的积、和.从而得出λ+μ=-1.
故选C.
点评:本题考查抛物线的性质和应用,解题时要注意向量和直线方程和合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目