Question

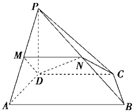如图，在四棱锥P-ABCD中，PD⊥底面ABCD，AD⊥AB，CD∥AB，AB=

2

AD=2，CD=3，直线PA与底面ABCD所成角为60°，点M、N分别是PA，PB的中点．
（1）求证：MN∥平面PCD；
（2）求证：四边形MNCD是直角梯形；
（3）求证：DN⊥平面PCB．

Answer 1

分析：（1）利用三角形的中位线性质证明MN∥AB，再由已知条件和公理4证明MN∥CD，再利用直线和平面平行
的判定定理证得MN∥平面PCD．
（2）由（1）可得MN∥CD．先由条件利用直线和平面垂直的判定证明CD⊥平面PAD，从而证得CD⊥MD，从而
得到四边形MNCD是直角梯形．
（3）由条件求得∠PAD=60°，利用勾股定理求得DN⊥CN．在Rt△PDB中，由PD=DB=

6

，N是PB的中点，
证得DN⊥PB，再根据直线和平面垂直的判定定理证得DN⊥平面PCB．

解答：证明：（1）因为点M，N分别是PA，PB的中点，所以MN∥AB．…（2分）
因为CD∥AB，所以MN∥CD．
又CD?平面PCD，而MN?平面PCD，所以MN∥平面PCD．…（4分）
（2）由（1）可得MN∥CD．
因为AD⊥AB，CD∥AB，所以CD⊥AD． 又因为PD⊥底面ABCD，CD?平面ABCD，
所以CD⊥PD，又AD∩PD=D，所以CD⊥平面PAD．…（6分）
因为MD?平面PAD，所以CD⊥MD，所以四边形MNCD是直角梯形．…（8分）
（3）因为PD⊥底面ABCD，所以∠PAD就是直线PA与底面ABCD所成的角，从而∠PAD=60°．  …（9分）
在Rt△PDA中，AD=2，PD=

6

，PA=2

2

，MD=

2

．
在直角梯形MNCD中，MN=1，ND=

3

，CD=3，CN=

MD2+(CD-MN)2

=

6

，
从而DN²+CN²=CD²，所以DN⊥CN．   …（11分）
连接BD，在Rt△PDB中，PD=DB=

6

，N是PB的中点，则DN⊥PB．…（13分）
又因为PB∩CN=N，所以DN⊥平面PCB．     …（14分）

点评：本题主要考查直线和平面平行的判定定理，以及直线和平面垂直的判定定理和性质性质定理的应用，
属于中档题．