题目内容

四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面，AB=a，BC=m，若在线段BC上存在点E满足PE⊥ED，则a的取值范围是
（0，
m
2
]
（0，
m
2
]
．
分析：先证明AE⊥ED，再利用三角形的相似，利用比例关系可得结论．
解答：解：连接AE，则
∵PA⊥底面ABCD，PE⊥ED，∴AE⊥ED
在矩形ABCD中，设BE=x，则CE=m-x，
∵△ABE∽△ECD
∴
AB
EC
=
BE
CD

∴a2=x（m-x）
∴x2-mx+a2=0，
∴△=m2-4a2≥0
∵a＞0，∴0＜a＜
m
2

∴0＜a＜
m
2
时，在线段BC上存在点E满足PE⊥ED，
故答案为：（0，
m
2
]
点评：本题考查线面垂直，考查三角形的相似，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
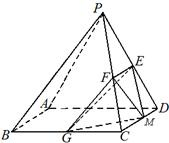精英家教网已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD⊥平面ABCD，E、F、G分别是PD、PC、BC的中点．
（I）求证：PA∥平面EFG；
（II）求平面EFG⊥平面PAD；
（III）若M是线段CD上一点，求三棱锥M-EFG的体积．
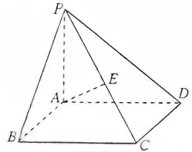（2012•上海）如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥底面ABCD，E是PC的中点，已知AB=2，AD=2
2
，PA=2，求：
（1）三角形PCD的面积；
（2）异面直线BC与AE所成的角的大小．
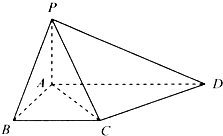如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，且AD∥BC，∠ABC=∠PAD=90°，侧面PAD⊥底面ABCD，若PA=AB=BC=
12
，AD=1．
（I）求证：CD⊥平面PAC
（II）求二面角A-PD-C的余弦值．
如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=90°，M为AB的中点．
（1）求证：BC∥平面PMD；
（2）求证：PC⊥BC；
（3）求点A到平面PBC的距离．
如图，在四棱锥P-ABCD中，底面ABCD为菱形，其中PA=PD=AD=2，∠BAD=60°，Q为AD的中点．
（1）求证：PA∥平面MDB；
（2）求证：AD⊥平面PQB；
（3）若平面PAD⊥平面ABCD，且M为PC的中点，求四棱锥M-ABCD的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网