题目内容
已知函数f(x)=cos2x-2sinxcosx-sin2x.
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)的最大值、最小值.
解:(Ⅰ)由题意,f(x)=cos2x-2sinxcosx-sin2x=cos2x-sin2x=
∴T=π;
(Ⅱ)当 ,即
,即 时,
时,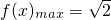 ;
;
当 ,即
,即 时,
时, .
.
分析:(Ⅰ)由题意,f(x)=cos2x-2sinxcosx-sin2x=cos2x-sin2x= ,从而可求函数周期;
,从而可求函数周期;
(Ⅱ)利用余弦函数取最值的条件,整体思考即可.
点评:本题以三角函数为载体,考查二倍角的余弦,考查函数的周期,同时考查了函数的最值,正确将函数化简是关键.

∴T=π;
(Ⅱ)当
 ,即
,即 时,
时,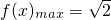 ;
; 当
 ,即
,即 时,
时, .
.分析:(Ⅰ)由题意,f(x)=cos2x-2sinxcosx-sin2x=cos2x-sin2x=
 ,从而可求函数周期;
,从而可求函数周期;(Ⅱ)利用余弦函数取最值的条件,整体思考即可.
点评:本题以三角函数为载体,考查二倍角的余弦,考查函数的周期,同时考查了函数的最值,正确将函数化简是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )