题目内容
在△ABC中,若 ,则sinB=
,则sinB=
- A.

- B.

- C.

- D.1
A
分析:先利用三角形内角和定理得 ,从而根据条件消去A,C,只保留角B,再求出sin
,从而根据条件消去A,C,只保留角B,再求出sin =
= ,从而问题解决.
,从而问题解决.
解答:∵A+B+C=π,
∴ ,
,
∴sin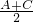 =cos
=cos ,
,
∵ ,
,
∴sinB=cos
即2sin cos
cos =cos
=cos
∴sin =
= ,从而cos
,从而cos =
=
∴sinB=2sin cos
cos =
= .
.
故选A.
点评:本题主要考查了三角函数的诱导公式、二倍角公式以及三角形内角和定理,属于基础题.
分析:先利用三角形内角和定理得
 ,从而根据条件消去A,C,只保留角B,再求出sin
,从而根据条件消去A,C,只保留角B,再求出sin =
= ,从而问题解决.
,从而问题解决.解答:∵A+B+C=π,
∴
 ,
,∴sin
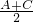 =cos
=cos ,
,∵
 ,
,∴sinB=cos

即2sin
 cos
cos =cos
=cos
∴sin
 =
= ,从而cos
,从而cos =
=
∴sinB=2sin
 cos
cos =
= .
.故选A.
点评:本题主要考查了三角函数的诱导公式、二倍角公式以及三角形内角和定理,属于基础题.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 ,则B的值为( )
,则B的值为( )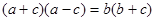 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.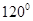 D.
D.
 ,则∠A=
,则∠A= 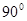 B.
B.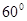 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2