题目内容
(本小题满分13分)已知椭圆 的两个焦点为
的两个焦点为 ,离心率为
,离心率为 ,直线l与椭圆相交于A、B两点,且满足
,直线l与椭圆相交于A、B两点,且满足 O为坐标原点.
O为坐标原点.
(1)求椭圆的方程;
(2)求 的最值.
的最值.
(1) ;(2)最小值为-2,最大值为2
;(2)最小值为-2,最大值为2
【解析】
试题分析:(1)由椭圆的离心率为 ,可得,
,可得, ,
,
即 .1分
.1分
又 ,
,
∴ 2分,
2分,
∴c=2,
∴ ,
,
∴椭圆方程为 3分
3分
(2)设直线AB的方程为y=kx+m,设 ,联立
,联立
 ,可得
,可得 ,
,
 ①
①
 5分
5分
∵ ,
,
∴ ,
,
∴ 6分,
6分,
又 ,
,
∴ ,
,
∴ ,
,
∴ , 8分,
, 8分,
 ,
,
∴ 10分
10分
当k=0(此时 满足①式).即直线AB平行于x轴时,
满足①式).即直线AB平行于x轴时, 的最小值为-2 .11分
的最小值为-2 .11分
当斜率不存在时,有 ,
,
∴ ,
,
将点A坐标代入椭圆方程,可得 ,
,
∴ ,
,
∴ 最大值为2,
最大值为2,
综上所述, 的最小值为-2,最大值为2 13分
的最小值为-2,最大值为2 13分
考点:本题考查椭圆的定义,椭圆的几何性质,直线与椭圆的位置关系

练习册系列答案
相关题目
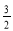 D.
D.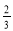
 中,
中, ,且
,且 ,则
,则 的最大值是( )
的最大值是( ) B.
B. C.
C. D.
D.
 共线,则t= .
共线,则t= .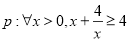 :命题
:命题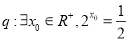 .则下列判断正确的是
.则下列判断正确的是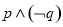 是真命题
是真命题 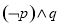 是真命题
是真命题
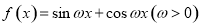 的最小正周期为
的最小正周期为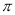 ,将
,将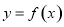 的图象向左平移
的图象向左平移 个单位得函数
个单位得函数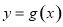 的图象,则
的图象,则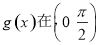 上单调递减
上单调递减  上单调递减
上单调递减
 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
