题目内容
 (2013•上海)如图,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为
(2013•上海)如图,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为| π | 6 |
分析:因为 CC1∥AA1.根据异面直线所成角的定义得∠BC1C为异面直线BC1与AA1所成的角,从而∠BC1C=
.在Rt△BC1C中,求得BC,从而求出S△ABC,最后利用柱体的体积公式即可求出该三棱柱的体积.
| π |
| 6 |
解答:解:因为 CC1∥AA1.
所以∠BC1C为异面直线BC1与AA1所成的角,即∠BC1C=
.
在Rt△BC1C中,BC=CC1tan∠BC1C=6×
=2
,
从而S△ABC=
BC2=3
,
因此该三棱柱的体积为V=S△ABC×AA1=3
×6=18
.
所以∠BC1C为异面直线BC1与AA1所成的角,即∠BC1C=
| π |
| 6 |
在Rt△BC1C中,BC=CC1tan∠BC1C=6×
| ||
| 3 |
| 3 |
从而S△ABC=
| ||
| 4 |
| 3 |
因此该三棱柱的体积为V=S△ABC×AA1=3
| 3 |
| 3 |
点评:本题考查三棱柱体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
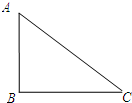 (2013•上海)如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积.
(2013•上海)如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积.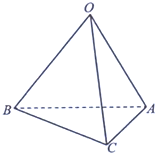 (2013•上海)如图,正三棱锥O-ABC的底面边长为2,高为1,求该三棱锥的体积及表面积.
(2013•上海)如图,正三棱锥O-ABC的底面边长为2,高为1,求该三棱锥的体积及表面积. (2013•上海)如图,已知双曲线C1:
(2013•上海)如图,已知双曲线C1: (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.