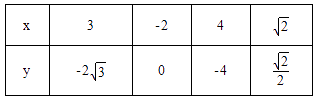
جâؤ؟ؤعبف
،¾جâؤ؟،؟بçح¼£¬شع؛£°¶دك ![]() ز»²àسذز»ذفدذسخہض³،£¬سخہض³،µؤا°ز»²؟·ض±ك½çخھاْدك¶خ
ز»²àسذز»ذفدذسخہض³،£¬سخہض³،µؤا°ز»²؟·ض±ك½çخھاْدك¶خ ![]() £¬¸أاْدك¶ختا؛¯ت
£¬¸أاْدك¶ختا؛¯ت ![]() £¬
£¬ ![]() µؤح¼دٌ£¬ح¼دٌµؤ×î¸كµمخھ
µؤح¼دٌ£¬ح¼دٌµؤ×î¸كµمخھ ![]() £®±ك½çµؤضذ¼ن²؟·ضخھ³¤1ا§أ×µؤض±دك¶خ
£®±ك½çµؤضذ¼ن²؟·ضخھ³¤1ا§أ×µؤض±دك¶خ ![]() £¬از
£¬از ![]() £®سخہض³،µؤ؛َز»²؟·ض±ك½çتازش
£®سخہض³،µؤ؛َز»²؟·ض±ك½çتازش ![]() خھش²ذؤµؤز»¶خش²»،
خھش²ذؤµؤز»¶خش²»، ![]() £®
£®
£¨1£©اَاْدك¶خ ![]() µؤ؛¯ت±ي´ïت½£»
µؤ؛¯ت±ي´ïت½£»
£¨2£©اْدك¶خ ![]() ةدµؤبë؟ع
ةدµؤبë؟ع ![]() ¾à؛£°¶دك
¾à؛£°¶دك ![]() ×î½ü¾àہëخھ1ا§أ×£¬دض×¼±¸´سبë؟ع
×î½ü¾àہëخھ1ا§أ×£¬دض×¼±¸´سبë؟ع ![]() ذقز»جُ±تض±µؤ¾°¹غآ·µ½
ذقز»جُ±تض±µؤ¾°¹غآ·µ½ ![]() £¬اَ¾°¹غآ·
£¬اَ¾°¹غآ· ![]() ³¤£»
³¤£»
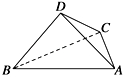
£¨3£©بçح¼£¬شعةبذخ ![]() اّسٍؤع½¨ز»¸ِئ½ذذثؤ±كذخذفدذاّ
اّسٍؤع½¨ز»¸ِئ½ذذثؤ±كذخذفدذاّ ![]() £¬ئ½ذذثؤ±كذخµؤز»±كشع؛£°¶دك
£¬ئ½ذذثؤ±كذخµؤز»±كشع؛£°¶دك ![]() ةد£¬ز»±كشع°ë¾¶
ةد£¬ز»±كشع°ë¾¶ ![]() ةد£¬ءيحâز»¸ِ¶¥µمPشعش²»،
ةد£¬ءيحâز»¸ِ¶¥µمPشعش²»، ![]() ةد£¬از
ةد£¬از ![]() £¬اَئ½ذذثؤ±كذخذفدذاّ
£¬اَئ½ذذثؤ±كذخذفدذاّ ![]() أو»µؤ×î´َضµ¼°´ثت±
أو»µؤ×î´َضµ¼°´ثت± ![]() µؤضµ£®
µؤضµ£®
،¾´ً°¸،؟
£¨1£©½â£؛سةزرضھجُ¼£¬µأ ![]()
سض،ك ![]()
سض،كµ± ![]() ت±£¬سذ
ت±£¬سذ ![]()
،à اْدك¶خ ![]() µؤ½âخِت½خھ
µؤ½âخِت½خھ ![]() £®
£®
£¨2£©½â£؛سة ![]() µأ
µأ
![]()
سض ![]()
![]()
،à ¾°¹غآ· ![]() ³¤خھ
³¤خھ ![]() ا§أ×
ا§أ×
£¨3£©½â£؛بçح¼£¬

![]()
×÷ ![]() ضلسع
ضلسع ![]() µم£¬شع
µم£¬شع ![]() ضذ£¬
ضذ£¬ ![]()
شع ![]() ضذ£¬
ضذ£¬ ![]()
،à ![]()
![]()
![]()
![]()
![]()
µ± ![]() ت±£¬¼´
ت±£¬¼´ ![]() ت±£؛ئ½ذذثؤ±كذخأو»×î´َضµخھ
ت±£؛ئ½ذذثؤ±كذخأو»×î´َضµخھ ![]()
،¾½âخِ،؟ض÷زھ؟¼²é¶ش؛¯تµؤشثسأ¼°¼¸؛خح¼ذخµؤس¦سأ¼°آك¼حئہيؤـء¦،£

،¾جâؤ؟،؟ر§ةْ»لخھءثµ÷²éر§ةْ¶ش2018ؤê¶يآقث¹تہ½ç±µؤ¹ط×¢تا·ٌسëذش±ًسذ¹ط£¬³éرùµ÷²é100بث£¬µأµ½بçدآت¾ف£؛
²»¹ط×¢ | ¹ط×¢ | ×ـ¼ئ | |
ؤذةْ | 30 | 15 | 45 |
إ®ةْ | 45 | 10 | 55 |
×ـ¼ئ | 75 | 25 | 100 |
¸ù¾ف±يضذت¾ف£¬ح¨¹¼ئثمح³¼ئء؟K2= ![]() £¬²¢²خ؟¼ز»دآءظ½çت¾ف£؛
£¬²¢²خ؟¼ز»دآءظ½çت¾ف£؛
P£¨K2£¾k0£© | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
بôسة´ثبدخھ،°ر§ةْ¶ش2018ؤê¶يآقث¹ؤêتہ½ç±µؤ¹ط×¢سëذش±ًسذ¹ط،±£¬شٍ´ث½لآغ³ِ´يµؤ¸إآت²»³¬¹£¨ £©
A.0.10
B.0.05
C.0.025
D.0.01