题目内容
如图所示,使电路接通,开关不同的开闭方式有( )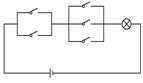
| A.11种 | B.20种 |
| C.21种 | D.12种 |
C
解析试题分析:设5个开关依次为1、2、3、4、5,由电路知识分析可得电路接通,则开关1、2与3、4、5中至少有1个接通,依次分析开关1、2与3、4、5中至少有1个接通的情况数目,由分步计数原理,计算可得答案.
解:根据题意,设5个开关依次为1、2、3、4、5,若电路接通,则开关1、2与3、4、5中至少有1个接通,对于开关1、2,共有2×2=4种情况,其中全部断开的有1种情况,则其至少有1个接通的有4-1=3种情况,对于开关3、4、5,共有2×2×2=8种情况,其中全部断开的有1种情况,则其至少有1个接通的8-1=7种情况,则电路接通的情况有3×7=21种;故选C.
考点:分步计数原理
点评:本题考查分步计数原理的应用,可以用间接法分析开关至少有一个闭合的情况,关键是分析出电路解题的条件.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有:
| A.210种 | B.420种 | C.630种 | D.840种 |
若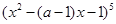 的展开式中没有x的奇次幂项,则含
的展开式中没有x的奇次幂项,则含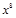 项的系数为( )
项的系数为( )
| A.5 | B.-5 | C.10 | D.-10 |
从甲地到乙地一天之中有三次航班,两趟火车,某人利用这两种交通工具在当天从甲地赶往乙地的方法有( )
| A.2种 | B.3种 | C.5种 | D.6种 |
三角形的三边均为整数,且最长的边为11,则这样的三角形的个数有( )个。
| A.25 | B.26 | C.32 | D.36 |
若 N
N
 ,且
,且 则
则 ( )
( )
| A.81 | B.16 | C. 8 | D.1 |
 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
如图所示,使电路接通,开关不同的开闭方法有( )
| A.11种 | B.20种 | C.21种 | D.12种 |