题目内容
已知椭圆的顶点与双曲线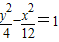 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为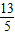 ,若椭圆的焦点在x轴上,求椭圆的标准方程.
,若椭圆的焦点在x轴上,求椭圆的标准方程.
【答案】分析:先求出双曲线的焦点及离心率,根据已知条件求出椭圆的离心率及焦距,利用椭圆的三个参数的关系,求出椭圆中的三个参数,求出椭圆的方程.
解答:解:设所求椭圆方程为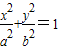 ,
,
其离心率为e,焦距为2c,
双曲线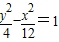 的焦距为2c1,离心率为e1,(2分)
的焦距为2c1,离心率为e1,(2分)
则有:c12=4+12=16,c1=4 (4分)
∴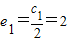 (6分)
(6分)
∴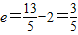 ,
,
即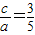 ①(8分)
①(8分)
又b=c1=4 ②(9分)
a2=b2+c2③(10分)
由①、②、③可得a2=25
∴所求椭圆方程为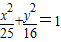 (12分)
(12分)
点评:本题考查椭圆双曲线的标准方程,以及简单性质的应用,用待定系数法求出椭圆标准方程是解题的关键.
解答:解:设所求椭圆方程为
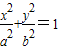 ,
,其离心率为e,焦距为2c,
双曲线
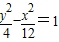 的焦距为2c1,离心率为e1,(2分)
的焦距为2c1,离心率为e1,(2分)则有:c12=4+12=16,c1=4 (4分)
∴
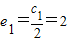 (6分)
(6分)∴
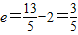 ,
,即
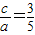 ①(8分)
①(8分)又b=c1=4 ②(9分)
a2=b2+c2③(10分)
由①、②、③可得a2=25
∴所求椭圆方程为
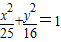 (12分)
(12分)点评:本题考查椭圆双曲线的标准方程,以及简单性质的应用,用待定系数法求出椭圆标准方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).