题目内容
设函数![]() (x∈[﹣π,π])的最大值为M,最小值为m,则M+m= .
(x∈[﹣π,π])的最大值为M,最小值为m,则M+m= .
考点:
函数最值的应用.
专题:
函数的性质及应用.
分析:
将函数化简,构造新函数g(x)=![]() (x∈[﹣π,π]),判断其为奇函数,可得g(x)max+g(x)min=0,从而可得结论.
(x∈[﹣π,π]),判断其为奇函数,可得g(x)max+g(x)min=0,从而可得结论.
解答:
解:![]() =
=![]() =2+
=2+![]()
令g(x)=![]() (x∈[﹣π,π]),则g(﹣x)=﹣g(x),∴函数g(x)是奇函数
(x∈[﹣π,π]),则g(﹣x)=﹣g(x),∴函数g(x)是奇函数
∴g(x)max+g(x)min=0
∴M+m=4+g(x)max+g(x)min=4
故答案为:4
点评:
本题考查函数的最值,考查函数的奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
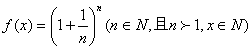 .
.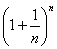 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;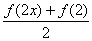 >
>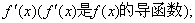
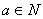 ,使得an<
,使得an<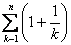 <
<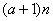 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.