题目内容
已知函数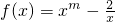 ,且f(2)=1.
,且f(2)=1.
(1)求m的值;
(2)判定f(x)的奇偶性,并说明理由;
(3)判断f(x)在(-∞,0)上的单调性并给予证明.
解:(1)因为f(2)=1,即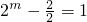 ,解得m=1.
,解得m=1.
(2)函数f(x)为奇函数.
函数 的定义域为{x|x≠0},关于原点对称.
的定义域为{x|x≠0},关于原点对称.
又因为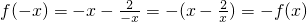 ,
,
所以f(x)是奇函数.
(3)设x1<x2<0,
则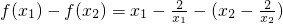 =
=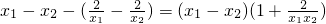 ,
,
因为x1<x2<0,所以x1-x2<0,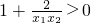 ,
,
所以f(x1)<f(x2),
因此f(x)在(-∞,0)上为单调增函数.
分析:(1)由f(2)=1列方程解出即可;
(2)根据函数奇偶性的定义即可作出判断;
(3)设x1<x2<0,通过作差可判断f(x1)与f(x2)的大小关系,依据单调性的定义即可判断;
点评:本题主要考查函数的表示方法及函数的单调性、奇偶性,属基础题,定义是解决该类问题的基本方法.
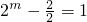 ,解得m=1.
,解得m=1.(2)函数f(x)为奇函数.
函数
 的定义域为{x|x≠0},关于原点对称.
的定义域为{x|x≠0},关于原点对称.又因为
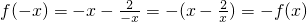 ,
,所以f(x)是奇函数.
(3)设x1<x2<0,
则
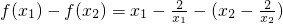 =
=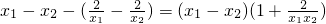 ,
,因为x1<x2<0,所以x1-x2<0,
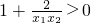 ,
,所以f(x1)<f(x2),
因此f(x)在(-∞,0)上为单调增函数.
分析:(1)由f(2)=1列方程解出即可;
(2)根据函数奇偶性的定义即可作出判断;
(3)设x1<x2<0,通过作差可判断f(x1)与f(x2)的大小关系,依据单调性的定义即可判断;
点评:本题主要考查函数的表示方法及函数的单调性、奇偶性,属基础题,定义是解决该类问题的基本方法.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
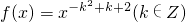 ,且f(2)<f(3)
,且f(2)<f(3)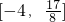 .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由.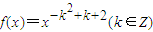 ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由. ,且f(2)<f(3)
,且f(2)<f(3) .若存在,求出这个p的值;若不存在,说明理由.
.若存在,求出这个p的值;若不存在,说明理由.