题目内容
某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,在将两组工人的日平均生产件数分成5组: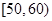 
,
,
,
,
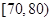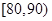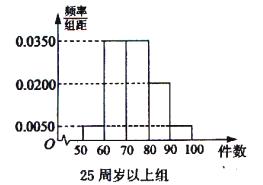
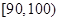分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的频率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成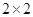
的列联表,并判断是否有
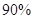的把握认为“生产能手与工人所在的年龄组有关”?
附表:
（1）0.7
（2）没有
的把握认为“生产能手与工人所在的年龄组有关”
解析试题分析：解:(Ⅰ)由已知得,样本中有 某大学一个专业团队为某专业大学生研究了多款学习软件，其中有A、B、C三种软件投入使用，经一学年使用后，团队调查了这个专业大一四个班的使用情况，从各班抽取的样本人数如下表 某研究性学习小组对昼夜温差与某种子发芽数的关系进行研究，他们分别记录了四天中每天昼夜温差与每天100粒种子浸泡后的发芽数，得到如下资料： “中国式过马路”存在很大的交通安全隐患．某调查机构为了解路人对“中国式过马路”的态度是否与性别有关，从马路旁随机抽取30名路人进行了问卷调查，得到了如下列联表： 为了考察某种中药预防流感效果，抽样调查40人，得到如下数据：服用中药的有20人，其中患流感的有2人，而未服用中药的20人中，患流感的有8人。
周岁以上组工人
名,周岁以下组工人
名
所以,样本中日平均生产件数不足件的工人中,周岁以上组工人有
(人),
记为
,
,
;周岁以下组工人有
(人),记为
,
从中随机抽取
名工人,所有可能的结果共有
种,
他们是:
,
,
,
,
,
,
,
,
,
其中,至少有名“周岁以下组”工人的可能结果共有
种,它们是:,,,,,,.
故所求的概率:
6分
(Ⅱ)由频率分布直方图可知,在抽取的
名工人中,“周岁以上组”中的生产能手
(人),“周岁以下组”中的生产能手
(人),据此可得
列联表如下: 生产能手 非生产能手 合计 周岁以上组
周岁以下组
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案
完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
（1）从这12人中随机抽取2人，求这2人恰好来自同一班级的概率．班级
一
二
三
四
人数
3
2
3
4
（2）从这12名学生中，指定甲、乙、丙三人为代表，已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是
，且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为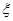
，求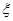的分布列和数学期望.
（1）求这四天浸泡种子的平均发芽率；时间
第一天
第二天
第三天
第四天
温差（℃）
9
10
8
11
发芽数（粒）
33
39
26
46
（2）若研究的一个项目在这四天中任选2天的种子发芽数来进行，记发芽的种子数分别为m，n（m＜n），则以（m，n）的形式列出所有的基本事件，并求“m，n满足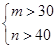
”的事件A的概率．
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 男性 女性 合计 反感 10 不反感 8 合计 30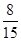 
．
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果，不需要写求解过程)，并据此资料分析反感“中国式过马路 ”与性别是否有关？
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动，记反感“中国式过马路”的人数为X，求X的分布列和数学期望．
下面的临界值表供参考：P(K2>k) 0.05 0.025 0.010 0.005 k 3.841 5.024 6.635 7.879
(参考公式：K2=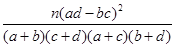
，其中n="a+b+c+d)"
（1）根据以上数据建立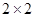
列联表；
（2）能否在犯错误不超过0.05的前提下认为该药物有效？
参考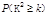
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
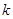
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
（
）
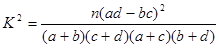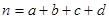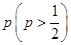，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为
.
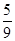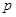的值；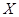
表示比赛停止时已比赛的局数，求随机变量
．
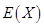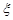的分布列和数学期望. 
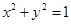相切的概率；
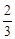，中奖可以获得2分；方案乙的中奖率为
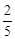，中奖可以获得3分；未中奖则不得分。每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品。
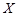,求
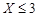的概率；