题目内容
18．已知C${\;}_{2013}^{1006}$+C${\;}_{2013}^{1007}$=C${\;}_{n}^{\frac{n}{2}}$，（2x-3）n=a0+a1（x-1）+a2（x-1）2+…+an（x-1）n，x∈R，n∈N*，则$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$的值为（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 由条件求得n=10，a0=1，在所给的等式中，令x=1+$\frac{1}{2}$，可得1+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$=0，即可求出$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$的值．
解答 解：∵C${\;}_{2013}^{1006}$+C${\;}_{2013}^{1007}$=C${\;}_{n}^{\frac{n}{2}}$，
∴n=2014，
∵（2x-3）n=（2x-3）2014=[-1+2（x-1）]2014=a0+a1（x-1）1+…an（x-1）n，x∈R，n∈N，∴a0=1．
在[-1+2（x-1）]2014=a0+a1（x-1）1+…an（x-1）n中，令x=1+$\frac{1}{2}$，可得1+$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$=0，
∴$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{n}}{{2}^{n}}$=-1，
故选：A．
点评 本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于中档题．
练习册系列答案
相关题目
9．点P坐标为（sinα-cosα，sinα+cosα），当α∈（0，2π）时，P在第二象限，则α取值范围为（ ）
| A． | （-$\frac{π}{4}$，$\frac{π}{4}$） | B． | （0，$\frac{π}{4}$）∪（$\frac{7π}{4}$，2π） | C． | （0，$\frac{π}{4}$）∪（$\frac{5π}{4}$，$\frac{7π}{4}$） | D． | （$\frac{π}{4}$，$\frac{3π}{4}$） |
6．
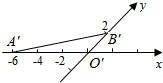如图，△O′A′B′是水平放置的△OAB的直观图，则△OAB的面积是（ ）
如图，△O′A′B′是水平放置的△OAB的直观图，则△OAB的面积是（ ）| A． | 6 | B． | 3$\sqrt{2}$ | C． | 6$\sqrt{2}$ | D． | 12 |