题目内容
定义在(-∞,0)∪(0,+∞)上的奇函数f(x)在(0,+∞)上为减函数,且f(2)=0,则“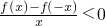 ”是
”是
“2x>4”成立的
- A.充分而不必要条件
- B.必要而不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
B
分析:先把两个命题M与N的解集解出看两集合A,B,若A?B则命题M是命题N的充分不必要条件,此题即是运用这种推理.
解答:∵f(x)定义在(-∞,0)∪(0,+∞)上的奇函数
∴f(x)-f(-x)=2f(x)
∴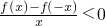 即
即
又∵f(x)在(0,+∞)上为减函数,且f(2)=0
∴x∈(2,+∞)
又∵f(x)定义在(-∞,0)∪(0,+∞)上的奇函数
∴x∈(2,+∞)∪(-∞,-2)
∵2x>4
∴x>2
∴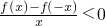 是2x>4的必要而不充分条件.
是2x>4的必要而不充分条件.
点评:充分条件、必要条件、充要条件是在构成许多数学命题时要用到的重要概念,但由于这些概念比较抽象,学生不易掌握,因此成了中学数学的难点之一.
分析:先把两个命题M与N的解集解出看两集合A,B,若A?B则命题M是命题N的充分不必要条件,此题即是运用这种推理.
解答:∵f(x)定义在(-∞,0)∪(0,+∞)上的奇函数
∴f(x)-f(-x)=2f(x)
∴
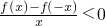 即
即
又∵f(x)在(0,+∞)上为减函数,且f(2)=0
∴x∈(2,+∞)
又∵f(x)定义在(-∞,0)∪(0,+∞)上的奇函数
∴x∈(2,+∞)∪(-∞,-2)
∵2x>4
∴x>2
∴
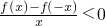 是2x>4的必要而不充分条件.
是2x>4的必要而不充分条件. 点评:充分条件、必要条件、充要条件是在构成许多数学命题时要用到的重要概念,但由于这些概念比较抽象,学生不易掌握,因此成了中学数学的难点之一.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
若定义在(-1,0)内的函数f(x)=log2a(x+1)>0,则a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、(
| ||
| D、(0,+∞) |