题目内容
已知定义在区间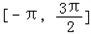 上的函数y=f(x)图象关于直线
上的函数y=f(x)图象关于直线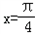 对称,当
对称,当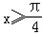 时,f(x)=﹣sinx.
时,f(x)=﹣sinx.
(1)作出y=f(x)的图象;
(2)求y=f(x)的解析式;
(3)若关于x的方程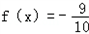 有解,将方程所有的解的和记为M,结合(1)中函数图象,求M的值.
有解,将方程所有的解的和记为M,结合(1)中函数图象,求M的值.
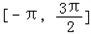 上的函数y=f(x)图象关于直线
上的函数y=f(x)图象关于直线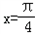 对称,当
对称,当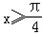 时,f(x)=﹣sinx.
时,f(x)=﹣sinx.(1)作出y=f(x)的图象;
(2)求y=f(x)的解析式;
(3)若关于x的方程
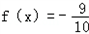 有解,将方程所有的解的和记为M,结合(1)中函数图象,求M的值.
有解,将方程所有的解的和记为M,结合(1)中函数图象,求M的值.
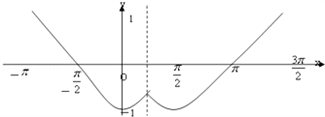
解:(1)y=f(x)的图象如图所示.
(2)任取x∈[﹣π,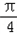 ],则
],则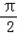 ﹣x∈[
﹣x∈[ ,
,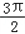 ],
],
由于函数f(x)图象关于直线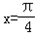 对称,则
对称,则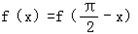 .
.
又当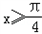 时,f(x)=﹣sinx,则
时,f(x)=﹣sinx,则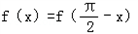 =﹣sin(
=﹣sin(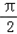 ﹣x)=﹣cosx,
﹣x)=﹣cosx,
 .
.
(3)因为﹣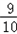 ∈(﹣1,﹣
∈(﹣1,﹣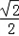 ),f(x)=﹣
),f(x)=﹣ 有4个根满足 x1<x2<
有4个根满足 x1<x2<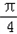 <x3<x4,
<x3<x4,
由对称性得,x1+x2=0,x3+x4=π,则M=x1+x2 +x3+x4=π.

(2)任取x∈[﹣π,
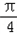 ],则
],则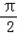 ﹣x∈[
﹣x∈[ ,
,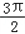 ],
],由于函数f(x)图象关于直线
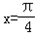 对称,则
对称,则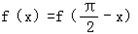 .
. 又当
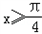 时,f(x)=﹣sinx,则
时,f(x)=﹣sinx,则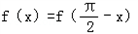 =﹣sin(
=﹣sin(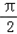 ﹣x)=﹣cosx,
﹣x)=﹣cosx, .
. (3)因为﹣
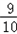 ∈(﹣1,﹣
∈(﹣1,﹣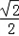 ),f(x)=﹣
),f(x)=﹣ 有4个根满足 x1<x2<
有4个根满足 x1<x2<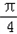 <x3<x4,
<x3<x4,由对称性得,x1+x2=0,x3+x4=π,则M=x1+x2 +x3+x4=π.

练习册系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)