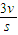题目内容
在平面内,三解形的面积为s,周长为c,则它的内切圆的半径r=
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R为( )
| 2s |
| c |
A.
| B.
| C.
| D.
|
结论:若三棱锥表面积为S,体积为V,则其内切球半径r=
”证明如下:
设三棱锥的四个面积分别为:S1,S2,S3,S4,
由于内切球到各面的距离等于内切球的半径
∴V=
S1×r+
S2×r+
S3×r+
S4×=
S×r
∴内切球半径r=
故选D.
| 3V |
| S |
设三棱锥的四个面积分别为:S1,S2,S3,S4,
由于内切球到各面的距离等于内切球的半径
∴V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴内切球半径r=
| 3V |
| S |
故选D.

练习册系列答案
相关题目
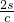 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R为
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R为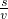

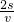
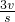
 .在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R为( )
.在空间中,三棱锥的体积为V,表面积为S,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R为( )