题目内容
函数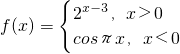
的图象上关于y轴对称的点共有
- A.1对
- B.2对
- C.3对
- D.4对
A
分析：考查函数y=2x-3（x＞0）关于y轴对称的函数为y=2-x-3（x＜0）为单调减函数，利用函数为y=2-x-3（x＜0）与y=cosπx（x＜0）有且只有一个交点，可得结论．
解答：考查函数y=2x-3（x＞0）关于y轴对称的函数为y=2-x-3（x＜0）为单调减函数
∵函数为y=2-x-3（x＜0）与y=cosπx（x＜0）有且只有一个交点
∴函数
的图象上关于y轴对称的点共有1对
故选A．
点评：本题考查函数图象的对称性，考查学生分析解决问题的能力，属于基础题．
分析：考查函数y=2x-3（x＞0）关于y轴对称的函数为y=2-x-3（x＜0）为单调减函数，利用函数为y=2-x-3（x＜0）与y=cosπx（x＜0）有且只有一个交点，可得结论．
解答：考查函数y=2x-3（x＞0）关于y轴对称的函数为y=2-x-3（x＜0）为单调减函数
∵函数为y=2-x-3（x＜0）与y=cosπx（x＜0）有且只有一个交点
∴函数
的图象上关于y轴对称的点共有1对故选A．
点评：本题考查函数图象的对称性，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
应用题作业本系列答案
相关题目