题目内容
【题目】已知数列{an}是公比不为1的等比数列，a1=1，且a1 ， a3 ， a2成等差数列．
（1）求数列{an}的通项；
（2）若数列{an}的前n项和为Sn ， 试求Sn的最大值．
【答案】
（1）解：设等比数列的公比为q，
∵a1，a3，a2成等差数列，
∴2a3=a1+a2，又a1=1，
∴2×1×q2=1+1×q，解得q=﹣ 
，或q=1（舍）．
∴ 
．
（2）解：由等比数列求和得，Sn=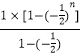 
= 
，
当n为奇数时， 
=1；
当n为偶数时， 
．
∴Sn的最大值为1．
【解析】（1）设等比数列的公比为q，由a1 ， a3 ， a2成等差数列，得2a3=a1+a2 ， 由通项公式可得q的方程，从而可求q，通项an；（2）由等比数列求和公式可得Sn ， 分n为奇数、偶数可得Sn的范围，从而可得结果；
【考点精析】利用数列的前n项和和等差数列的性质对题目进行判断即可得到答案，需要熟知数列{an}的前n项和sn与通项an的关系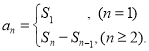
；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列．
练习册系列答案
相关题目
