题目内容
设函数 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( )
A. 在 在 单调递减 单调递减 | B. 在 在 单调递减 单调递减 |
C. 在 在 单调递增 单调递增 | D. 在 在 单调递增 单调递增 |
A
解析试题分析:因为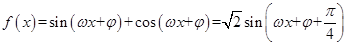 ,因为f(x)的最小正周期为
,因为f(x)的最小正周期为 ,所以
,所以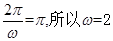 ,又因为
,又因为 ,所以
,所以 ,因为
,因为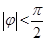 ,所以
,所以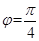 ,所以
,所以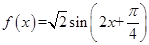 ,所以
,所以 在
在 单调递减。
单调递减。
考点:和差公式;三角函数的周期公式;函数的奇偶性。
点评:求三角函数的周期和单调区间时,一般把函数化为y=Asin(ωx+φ)的形式,在求单调区间时,一定要注意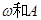 的正负。
的正负。

练习册系列答案
相关题目
若函数 的图象(部分)如图所示,则
的图象(部分)如图所示,则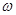 和
和 的取值是
的取值是 
A. | B. |
C.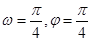 | D. |
要得到函数 的图像, 需要将函数
的图像, 需要将函数 的图像( )
的图像( )
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
当 时,函数
时,函数 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点 对称 对称 | B.偶函数且图像关于点 对称 对称 |
C.奇函数且图像关于直线 对称 对称 | D.偶函数且图像关于点 对称 对称 |
给定性质: ①最小正周期为π;②图象关于直线x=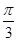 对称,则下列四个函数中,
对称,则下列四个函数中,
同时具有性质①、②的是( )
A.y = sin(2x- ) ) | B.y = sin( + + ) ) |
C.y = sin(2x+ ) ) | D.y = sin|x| |
已知 ,且
,且 是第四象限的角,则
是第四象限的角,则 =( )
=( )
A. | B. | C.- | D.- |
 为锐角三角形,则
为锐角三角形,则

则 与
与 的大小关系为( )。
的大小关系为( )。
A. | B. | C. | D. |
若角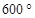 的终边上有一点
的终边上有一点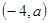 ,则
,则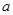 的值是.
的值是.
A. | B. | C. | D. |
若角 的终边上有一点
的终边上有一点 ,则
,则 的值是( ).
的值是( ).
A. | B. | C. | D. |