题目内容
设集合,A={(x,y)|(x﹣t)2+(y﹣at+2)2=1}和集合B={(x,y)|(x﹣4)2+y2=1},如果命题“?t∈R,A∩B≠∅”是真命题,则实数a的取值范围是( )
A.0<a≤ | B.0≤a≤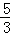 | C.0≤a≤ | D.0≤a<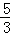 |
C
解析试题分析:集合A表示以(t,at-2)为圆心,半径为1的圆上的点的集合,集合B表示以(4,0)为圆心,半径为1的圆上的点的集合,因为A∩B≠∅所以两圆有公共点,则两圆心距离不大于两半径和即 ,得到关于t的一个一元二次方程(含参数a)
,得到关于t的一个一元二次方程(含参数a) 即
即 有解,所以
有解,所以 ,解得
,解得 ,答案选C.
,答案选C.
考点:命题与集合的运算

练习册系列答案
相关题目
集合A={0,1,2,3,4},B={x|x<2},则A∩B=( ).
A. | B.{0,1} | C.{0,1,2} | D.{x|x<2} |
 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
设 则( ).
则( ).
A. | B. | C. | D. |
 是整数集的一个非空子集,对于
是整数集的一个非空子集,对于 ,若
,若 ,且
,且 ,则称
,则称 是
是 的一个“孤立元”。给定集合
的一个“孤立元”。给定集合 ,在由
,在由 的三个元素构成的所有集合中,不含“孤立元”的集合个数为 .
的三个元素构成的所有集合中,不含“孤立元”的集合个数为 .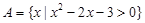 ,
, .
. ,使得
,使得 ,求
,求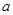 的取值范围;
的取值范围;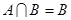 ,求
,求 ,集合
,集合
 ,求集合
,求集合 ; (2)若
; (2)若 ,求实数
,求实数 的取值范围
的取值范围  ,集合
,集合 ,则
,则 ( )
( )



 的子集个数为________
的子集个数为________