题目内容
曲线f(x)=ωsinωx+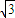 ωcosωx(ω>0,x∈R)上的一个最大值点为P,一个最小值点为Q,则P、Q两点间的距离|PQ|的最小值是( )
ωcosωx(ω>0,x∈R)上的一个最大值点为P,一个最小值点为Q,则P、Q两点间的距离|PQ|的最小值是( )A.
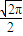
B.
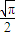
C.2

D.2
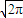
【答案】分析:由两角和的正弦公式化简f(x)的解析式为2ωsin(ωx+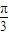 ),由题意求出P、Q两点间的坐标,再利用两点间的距离公式求出|PQ|的表达式,再运用基本不等式求出其最小值.
),由题意求出P、Q两点间的坐标,再利用两点间的距离公式求出|PQ|的表达式,再运用基本不等式求出其最小值.
解答:解:f(x)=ωsinωx+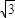 ωcosωx=2ω(
ωcosωx=2ω( +
+ )=2ωsin(ωx+
)=2ωsin(ωx+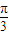 ),
),
令ωx+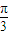 =
=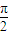 ,可得x=
,可得x=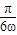 ,故可令点P的坐标为(
,故可令点P的坐标为(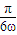 ,2ω).
,2ω).
再令ωx+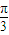 =
=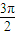 ,可得x=
,可得x= ,故可令点Q的坐标为(
,故可令点Q的坐标为( ,-2ω).
,-2ω).
则P、Q两点间的距离|PQ|= =
= ≥
≥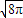 =2
=2 ,
,
当且仅当 =4ω,即ω=
=4ω,即ω=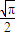 时,等号成立.
时,等号成立.
故P、Q两点间的距离|PQ|的最小值是2 ,
,
故选D.
点评:本题主要考查两角和的正弦公式,基本不等式的应用,式子的变形是解题的关键,属于基础题.
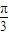 ),由题意求出P、Q两点间的坐标,再利用两点间的距离公式求出|PQ|的表达式,再运用基本不等式求出其最小值.
),由题意求出P、Q两点间的坐标,再利用两点间的距离公式求出|PQ|的表达式,再运用基本不等式求出其最小值.解答:解:f(x)=ωsinωx+
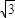 ωcosωx=2ω(
ωcosωx=2ω( +
+ )=2ωsin(ωx+
)=2ωsin(ωx+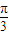 ),
),令ωx+
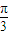 =
=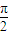 ,可得x=
,可得x=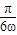 ,故可令点P的坐标为(
,故可令点P的坐标为(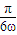 ,2ω).
,2ω).再令ωx+
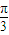 =
=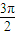 ,可得x=
,可得x= ,故可令点Q的坐标为(
,故可令点Q的坐标为( ,-2ω).
,-2ω).则P、Q两点间的距离|PQ|=
 =
= ≥
≥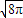 =2
=2 ,
,当且仅当
 =4ω,即ω=
=4ω,即ω=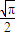 时,等号成立.
时,等号成立.故P、Q两点间的距离|PQ|的最小值是2
 ,
,故选D.
点评:本题主要考查两角和的正弦公式,基本不等式的应用,式子的变形是解题的关键,属于基础题.

练习册系列答案
相关题目
 如图,已知曲线
如图,已知曲线