题目内容
设 是定义在
是定义在 上的以
上的以 为周期的奇函数,若
为周期的奇函数,若 ,则实数
,则实数 的取值范围
的取值范围
是( )
 是定义在
是定义在 上的以
上的以 为周期的奇函数,若
为周期的奇函数,若 ,则实数
,则实数 的取值范围
的取值范围是( )
A. | B. | C. | D. |
C
根据周期为3,得到f(-2)=f(1),根据函数为奇函数,得到f(-2)=-f(2),从而求出a的取值范围.
解:f(x)是定义在R上的以3为周期的奇函数,
∴f(-2)=f(-2+3)=f(1)>1
而f(-2)=-f(2)= >1
>1
解得-1<a<
故选C.
解:f(x)是定义在R上的以3为周期的奇函数,
∴f(-2)=f(-2+3)=f(1)>1
而f(-2)=-f(2)=
 >1
>1解得-1<a<

故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 是偶函数,它在
是偶函数,它在 上是增函数.若
上是增函数.若 则
则 的取值范围是( )
的取值范围是( )



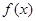 在定义域R上不是常数函数,且
在定义域R上不是常数函数,且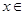 R,
R,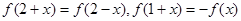 ,则
,则 是定义域为
是定义域为 的奇函数,且
的奇函数,且 对称,那么下列式子中对任意
对称,那么下列式子中对任意 恒成立的是
恒成立的是 



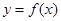 是偶函数,当
是偶函数,当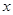 >0 时,
>0 时,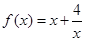 ,且当
,且当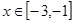 时,
时,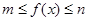 成立,则
成立,则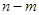 的最小值为
的最小值为 B.
B.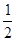 C.
C. 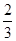 D. 1
D. 1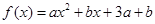 是偶函数,且定义域为
是偶函数,且定义域为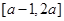 ,则
,则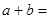 _______
_______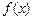 =
=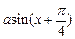 +
+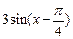 是偶函数,则实数a= .
是偶函数,则实数a= .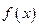 是奇函数,当
是奇函数,当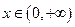 时,
时,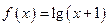 ,则当
,则当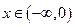 时,
时,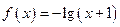
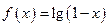
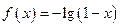
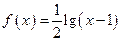
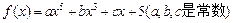 ,且
,且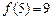 ,则
,则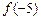 的值为 ▲ .
的值为 ▲ .