题目内容
分别求出下列条件确定的圆的方程:
(1)圆心为M(3,-5),且经过点P(7,-2)
(2)圆心在x轴上,半径长是5,且与直线x-6=0相切.
(1)圆心为M(3,-5),且经过点P(7,-2)
(2)圆心在x轴上,半径长是5,且与直线x-6=0相切.
分析:(1)设圆的标准方程为(x-3)2+(y+5)2=r2,将点P坐标代入求出r的值,即可得到所求圆的标准方程.
(2)根据圆心在x轴上且半径长是5,设圆的标准方程为(x-a)2+y2=52,再由圆与直线x-6=0相切建立关于a的等式,解出a=1或a=11,即可得到所求圆的标准方程.
(2)根据圆心在x轴上且半径长是5,设圆的标准方程为(x-a)2+y2=52,再由圆与直线x-6=0相切建立关于a的等式,解出a=1或a=11,即可得到所求圆的标准方程.
解答:解:(1)∵圆心为M(3,-5),∴设圆的方程为(x-3)2+(y+5)2=r2,
∵点P(7,-2)在圆上,
∴将P的坐标代入,得(7-3)2+(-2+5)2=r2,解之得r=5
由此可得圆的标准方程为:(x-3)2+(y+5)2=25;
(2)∵圆心在x轴上,半径长是5,
∴设圆的标准方程为(x-a)2+y2=25,
∵圆与直线x-6=0相切,
∴圆心到直线x-6=0的距离等于半径,即|a-6|=5,解之得a=1或a=11
因此,圆的标准方程为:(x-1)2+y2=25或 (x-11)2+y2=25.
∵点P(7,-2)在圆上,
∴将P的坐标代入,得(7-3)2+(-2+5)2=r2,解之得r=5
由此可得圆的标准方程为:(x-3)2+(y+5)2=25;
(2)∵圆心在x轴上,半径长是5,
∴设圆的标准方程为(x-a)2+y2=25,
∵圆与直线x-6=0相切,
∴圆心到直线x-6=0的距离等于半径,即|a-6|=5,解之得a=1或a=11
因此,圆的标准方程为:(x-1)2+y2=25或 (x-11)2+y2=25.
点评:本题给出满足条件的圆,求圆的方程.着重考查了圆的标准方程、直线与圆的位置关系等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量
 且
且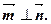
 的大小;
的大小; ②
② ③
③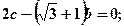 ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 的面积.
的面积. 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量
 且
且
 的大小;
的大小; ②
② ③
③ ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 的面积.
的面积. 的三个内角A,B,C所对的边分别为a,b,c,
向量
的三个内角A,B,C所对的边分别为a,b,c,
向量
 且
且
 的大小;
的大小; ②
② ③
③ ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定 的面积.
的面积. =(-1,1),
=(-1,1), =(cosBcosC,sinBsinC-
=(cosBcosC,sinBsinC- ),且
),且 。
。 +1)b=0;④B=45°。试从中再选择两个条件以确定△ABC,求出你所确定的△ABC的面积。
+1)b=0;④B=45°。试从中再选择两个条件以确定△ABC,求出你所确定的△ABC的面积。