题目内容
已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y),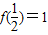 ,如果对于0<x<y,都有f(x)>f(y).
,如果对于0<x<y,都有f(x)>f(y).(1)求f(1);
(2)解不等式f(-x)+f(3-x)≥-2.
【答案】分析:(1)用赋值法令x=y=1 f(1)=0
(2)由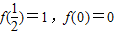 ,将-2表示为f(4),再将f(-x)+f(3-x)转化为f[x(x-3)],原不不等式f(-x)+f(3-x)≥-2.转化为f[x(x-3)],≥f(4),再利单调性定义求解.
,将-2表示为f(4),再将f(-x)+f(3-x)转化为f[x(x-3)],原不不等式f(-x)+f(3-x)≥-2.转化为f[x(x-3)],≥f(4),再利单调性定义求解.
解答:解:(1)令x=y=1得f(1)=f(1)+f(1)⇒f(1)=0(4分)
(2)由f( )=1,f(1)=0,
)=1,f(1)=0,
结合题意,可得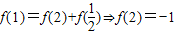 (6分)
(6分)
f(4)=f(2)+f(2)=-2(8分)∴f(-x)+f(3-x)=f[x(x-3)]≥f(4)(10分)
又f(x)为(0,+∞)上的减函数
∴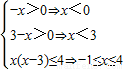 (14分)
(14分)
解得-1≤x<0
∴原不等式的解集为[-1,0).(16分)
点评:本题主要考查抽象函数中的赋值法和单调性定义的应用.
(2)由
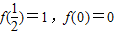 ,将-2表示为f(4),再将f(-x)+f(3-x)转化为f[x(x-3)],原不不等式f(-x)+f(3-x)≥-2.转化为f[x(x-3)],≥f(4),再利单调性定义求解.
,将-2表示为f(4),再将f(-x)+f(3-x)转化为f[x(x-3)],原不不等式f(-x)+f(3-x)≥-2.转化为f[x(x-3)],≥f(4),再利单调性定义求解.解答:解:(1)令x=y=1得f(1)=f(1)+f(1)⇒f(1)=0(4分)
(2)由f(
 )=1,f(1)=0,
)=1,f(1)=0,结合题意,可得
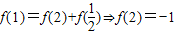 (6分)
(6分)f(4)=f(2)+f(2)=-2(8分)∴f(-x)+f(3-x)=f[x(x-3)]≥f(4)(10分)
又f(x)为(0,+∞)上的减函数
∴
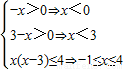 (14分)
(14分)解得-1≤x<0
∴原不等式的解集为[-1,0).(16分)
点评:本题主要考查抽象函数中的赋值法和单调性定义的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
