题目内容
已知函数f(x)=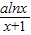 +
+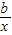 ,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.
,曲线y=f(x)在点(1,f(1))处的切线方程为x+2y-3=0.(Ⅰ)求a、b的值;
(Ⅱ)如果当x>0,且x≠1时,f(x)>
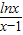 +
+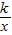 ,求k的取值范围.
,求k的取值范围.
【答案】分析:(I)求出函数的导数;利用切线方程求出切线的斜率及切点;利用函数在切点处的导数值为曲线切线的斜率及切点也在曲线上,列出方程组,求出a,b值.
(II)将不等式变形,构造新函数,求出新函数的导数,对参数k分类讨论,判断出导函数的符号,得到函数的单调性,求出函数的最值,求出参数k的范围.
解答:解:由题意f(1)=1,即切点坐标是(1,1)
(Ⅰ)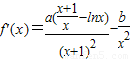
由于直线x+2y-3=0的斜率为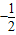 ,且过点(1,1),故
,且过点(1,1),故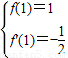
即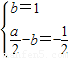 解得a=1,b=1.
解得a=1,b=1.
(Ⅱ)由(Ⅰ)知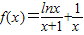 ,所以
,所以
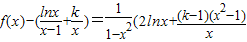 ).
).
考虑函数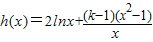 (x>0),则
(x>0),则
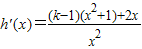 .
.
(i)设k≤0,由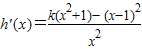 知,当x≠1时,h′(x)<0.而h(1)=0,故
知,当x≠1时,h′(x)<0.而h(1)=0,故
当x∈(0,1)时,h′(x)<0,可得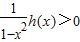 ;
;
当x∈(1,+∞)时,h′(x)<0,可得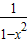 h(x)>0
h(x)>0
从而当x>0,且x≠1时,f(x)-(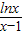 +
+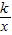 )>0,即f(x)>
)>0,即f(x)>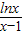 +
+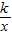 .
.
(ii)设0<k<1.由于当x∈(1,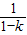 )时,(k-1)(x2+1)+2x>0,故h′(x)>0,而
)时,(k-1)(x2+1)+2x>0,故h′(x)>0,而
h(1)=0,故当x∈(1,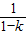 )时,h(x)>0,可得
)时,h(x)>0,可得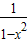 h(x)<0,与题设矛盾.
h(x)<0,与题设矛盾.
(iii)设k≥1.此时h′(x)>0,而h(1)=0,故当x∈(1,+∞)时,h(x)>0,可得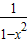 h(x)<0,与题设矛盾.
h(x)<0,与题设矛盾.
综合得,k的取值范围为(-∞,0]
点评:本题考查导数的几何意义:函数在切点处的导数值是切线的斜率、考查构造函数,通过导数研究函数的单调性,求出函数的最值、考查发了讨论的数学思想方法.
(II)将不等式变形,构造新函数,求出新函数的导数,对参数k分类讨论,判断出导函数的符号,得到函数的单调性,求出函数的最值,求出参数k的范围.
解答:解:由题意f(1)=1,即切点坐标是(1,1)
(Ⅰ)
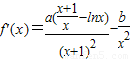
由于直线x+2y-3=0的斜率为
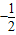 ,且过点(1,1),故
,且过点(1,1),故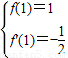
即
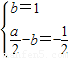 解得a=1,b=1.
解得a=1,b=1.(Ⅱ)由(Ⅰ)知
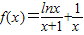 ,所以
,所以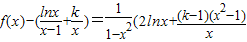 ).
).考虑函数
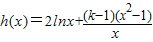 (x>0),则
(x>0),则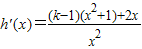 .
.(i)设k≤0,由
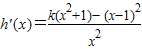 知,当x≠1时,h′(x)<0.而h(1)=0,故
知,当x≠1时,h′(x)<0.而h(1)=0,故当x∈(0,1)时,h′(x)<0,可得
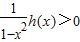 ;
;当x∈(1,+∞)时,h′(x)<0,可得
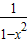 h(x)>0
h(x)>0从而当x>0,且x≠1时,f(x)-(
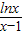 +
+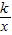 )>0,即f(x)>
)>0,即f(x)>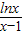 +
+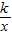 .
.(ii)设0<k<1.由于当x∈(1,
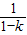 )时,(k-1)(x2+1)+2x>0,故h′(x)>0,而
)时,(k-1)(x2+1)+2x>0,故h′(x)>0,而h(1)=0,故当x∈(1,
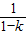 )时,h(x)>0,可得
)时,h(x)>0,可得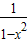 h(x)<0,与题设矛盾.
h(x)<0,与题设矛盾.(iii)设k≥1.此时h′(x)>0,而h(1)=0,故当x∈(1,+∞)时,h(x)>0,可得
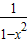 h(x)<0,与题设矛盾.
h(x)<0,与题设矛盾.综合得,k的取值范围为(-∞,0]
点评:本题考查导数的几何意义:函数在切点处的导数值是切线的斜率、考查构造函数,通过导数研究函数的单调性,求出函数的最值、考查发了讨论的数学思想方法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|