题目内容
已知非零向量 、
、 满足|
满足| +
+ |=|
|=| -
- |=
|= |
| |,则
|,则 +
+ 与
与 -
- 的夹角为
的夹角为
- A.30°
- B.60°
- C.120°
- D.150°
B
分析:欲求( +
+ )与(
)与( -
- )的夹角,根据公式cos<
)的夹角,根据公式cos< ,
, >=
>= ,需表示(
,需表示( +
+ )(
)( -
- )及|
)及| +
+ |•|
|•| -
- |;由于|
|;由于| +
+ |•|
|•| -
- |易于用|
|易于用| |表示,所以考虑把(
|表示,所以考虑把( +
+ )(
)( -
- )也用|
)也用| |表示,这需要把已知等式都平方整理即可.
|表示,这需要把已知等式都平方整理即可.
解答:∵| +
+ |=|
|=| -
- |=
|= |
| |
|
∴( +
+ )2=(
)2=( -
- )2=
)2=
 2 整理得
2 整理得 •
• =0,
=0, 2=
2=
 2.
2.
设( +
+ )与(
)与( -
- )的夹角为α,
)的夹角为α,
则( +
+ )(
)( -
- )=|
)=| +
+ |•|
|•| -
- |cosα=
|cosα=
 2cosα,且(
2cosα,且( +
+ )(
)( -
- )=
)= 2-
2- 2=
2=
 2.
2.
∴cosα= ,解得α=60°.
,解得α=60°.
故选B.
点评:向量夹角问题的解决:一般需在公式cos< ,
, >=
>= 的基础上,再考虑
的基础上,再考虑 •
• 的化简.
的化简.
分析:欲求(
 +
+ )与(
)与( -
- )的夹角,根据公式cos<
)的夹角,根据公式cos< ,
, >=
>= ,需表示(
,需表示( +
+ )(
)( -
- )及|
)及| +
+ |•|
|•| -
- |;由于|
|;由于| +
+ |•|
|•| -
- |易于用|
|易于用| |表示,所以考虑把(
|表示,所以考虑把( +
+ )(
)( -
- )也用|
)也用| |表示,这需要把已知等式都平方整理即可.
|表示,这需要把已知等式都平方整理即可.解答:∵|
 +
+ |=|
|=| -
- |=
|= |
| |
|∴(
 +
+ )2=(
)2=( -
- )2=
)2=
 2 整理得
2 整理得 •
• =0,
=0, 2=
2=
 2.
2.设(
 +
+ )与(
)与( -
- )的夹角为α,
)的夹角为α,则(
 +
+ )(
)( -
- )=|
)=| +
+ |•|
|•| -
- |cosα=
|cosα=
 2cosα,且(
2cosα,且( +
+ )(
)( -
- )=
)= 2-
2- 2=
2=
 2.
2.∴cosα=
 ,解得α=60°.
,解得α=60°.故选B.
点评:向量夹角问题的解决:一般需在公式cos<
 ,
, >=
>= 的基础上,再考虑
的基础上,再考虑 •
• 的化简.
的化简. 
练习册系列答案
相关题目
 )·
)·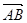 与
与 满足(
满足(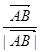 +
+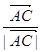 )·
)· =0,且
=0,且
 、
、 满足
满足 ,那么向量
,那么向量 与向量
与向量 的夹角为
的夹角为 B.
B. C.
C. D.
D.
 和
和 满足
满足 ,且
,且 ,
,